Nine Chapter Dynamic Programming¶
Lecture 1 Introduction to Dynamic Programming¶
| Problem | Category |
|---|---|
| Coin Change | |
| Unique Paths | coordinate |
| Jump Game |
- 动态规划题目特点:
- 计数
- 有多少种方式走到右下角
- 有多少种方法选出k个数使得和是Sum
- 求最大最小值
- 从左上角走到右下角路径的最大数字和
- 最长上升子序列长度
- 求存在性
- 取石子游戏,先手是否必胜
- 能不能选出k个数使得和是Sum
- 计数
- 状态是动态规划定海神针,确定状态需要两个基本意识:
- 最后一步
- 子问题
Four Ingredients for DP
- What's the state?
- start with the last step for the optimal solution
- decompose into subproblems
- Write the state transition?
- find the transition from subproblem relations
- Initial value and boundary conditions
- need to think careful in this step
- How can you compute the states?
- iteration directio
- forward computing
Coin Change¶
- Imagine the last coin you can use and the minimum solution to found can be represented as
f[amount]. It can be solved by solving the smaller problem first. we havef[amount] = min(f[amount], f[amount - last_coin] + 1). - The problem is we don't know which coin will be selected for the last one to reach the solution, so we have to iterate through the coins to check every one of them. We expecting to see two
forloops in our code. - DP 4 ingredient:
- size of the dp array
f[amount + 1] - initial state:
f[0] = 0, amount 0 can use 0 coin. - subproblem:
f[amount] = min(f[amount], f[amount - last\_coin] + 1). - results:
f[amount]
- size of the dp array
class Solution {
public:
int coinChange(vector<int>& coins , int amount) {
int n = coins.size();
int f[amount + 1];
f[0] = 0;
/* calculate the f[1], f[2], ... f[amount] */
for (int i = 1; i <= amount; i++) {
f[i] = INT_MAX; /* small trick, set to invalid first */
for (int j = 0; j < n; j++) { /* update states */
/* f[i] can select coins[j] && f[i - coins[j]] is possible && coins[j] is last coin */
if (i >= coins[j] && f[i - coins[j]] != INT_MAX && f[i - coins[j]] + 1 < f[i]) {
f[i] = f[i - coins[j]] + 1;
}
}
}
return f[amount] == INT_MAX ? -1 : f[amount];
}
};
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
int f[amount+1];
// f[i] represent the minimum counts to make up i amount
// use INT_MAX to represent impossible case.
f[0] = 0;
for (int i = 1; i <= amount; i++) {
f[i] = INT_MAX;
for (int j = 0; j < n; j++) {
if (i >= coins[j] && f[i - coins[j]] != INT_MAX) {
f[i] = min(f[i], f[i - coins[j]] + 1);
}
}
}
return f[amount] == INT_MAX ? -1 : f[amount];
}
};
Unique Paths¶
- Solving smaller problem first than by accumulating the results from the smaller problems, we can solve the overall problem.
- Use a 2-d array to record the result the smaller problem, we know for the position
f[i][j] = f[i - 1][j] + f[i][j - 1], which means the summation of number of path from above and from left. - The initial state is the first row and the first column are all equal to
1.
class Solution {
public:
/**
* @param n, m: positive integer (1 <= n ,m <= 100)
* @return an integer
*/
int uniquePaths(int m, int n) {
int f[m][n] = {0};
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 || j == 0) {
f[i][j] = 1;
}
if (i > 0 && j > 0) {
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
}
}
return f[m - 1][n - 1];
}
};
Jump Game¶
- Notice the problem statement "Each element in the array represents your maximum jump length at that position."
Solution 1 DP
- The problem have characteristics of the dynamic problem, that is it can be decomposed into smaller problem, the large problem can be solved using the result from solving smaller problems.
- We use a dp array
f[i]to store whether it can jump from previous position to positioni. ifnums[i] + i >= j, it can also jump to positionj. - Looks like we are going to have a nested loop. the outer loop iterate to check whether can jump to each step
j. inner loop check each step beforej, namely the smaller size problem.
class Solution {
public:
bool canJump(vector<int>& nums) {
int n = nums.size();
if (n == 0)
return true;
int f[n];
f[0] = true; /* initialize */
for (int j = 1; j < n; j++) {
f[j] = false;
for (int i = 0; i < j; i++) {
if (f[i] && nums[i] + i >= j) {
f[j] = true;
break;
}
}
}
return f[n - 1];
}
};
Solution 2 Greedy
- Use a variable
cur_maxto maintain the possible maximum jump position, if the current position is less than the maximum possible jump, return flase.
class Solution {
public:
bool canJump(vector<int>& nums) {
int n = nums.size();
if (n == 0)
return true;
int cur_max = nums[0]; /* maximum distance can reach from ith */
/* L.I.: current step (ith step) must <= cur_max jump */
for (int i = 0; i < n; i++) {
if (i > cur_max) /* must goes first */
return false;
if (i + nums[i] > cur_max)
cur_max = i + nums[i];
}
return true;
}
};
Lecture 2 Dynamic Programming on Coordinates¶
| Problem | Category |
|---|---|
| Unique Paths II | 坐标型 |
| Paint House | 序列型 + 状态 |
| Decode Ways | 划分型 |
| Longest Increasing Continuous Subsequence | 序列型 / 划分型 |
| Minimum Path Sum | 坐标型 |
| Bomb Enemy | 坐标型 |
| Counting Bits | 坐标型 |
坐标型动态规划¶
- 最简单的动态规划类型
- 给定一个序列或网格
- 需要找到序列中某个/些子序列或网格中的某条路径
- 某种性质最大/最小
- 计数
- 存在性
- 动态规划方程
f[i]中的下标i表示以a[i]为结尾的满足条件的子序列的性质.f[i][j]中的 下标i,j表示以格子(i, j)为结尾的满足条件的路径的性质- 最大值/最小值
- 个数
- 是否存在
- 坐标型动态规划的初始条件
f[0]就是指以a[0]为结尾的子序列的性质
Unique Paths II¶
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
int i = 0;
int j = 0;
int flag = 0;
vector<vector<int>> f(m, vector<int>(n));
if (m == 0 || n == 0) {
return 0;
}
if (obstacleGrid[0][0] == 1) {
return 0;
}
f[0][0] = 1;
for (i = 1; i < m; i++) {
if (obstacleGrid[i][0] == 1) {
f[i][0] = 0;
} else {
f[i][0] = f[i-1][0];
}
}
for (j = 1; j < n; j++) {
if (obstacleGrid[0][j] == 1) {
f[0][j] = 0;
} else {
f[0][j] = f[0][j-1];
}
}
for (i = 1; i < m; i++) {
for (j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) {
f[i][j] = 0;
} else {
f[i][j] = f[i][j-1] + f[i-1][j];
}
}
}
return f[m-1][n-1];
}
};
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = m > 0 ? obstacleGrid[0].size() : 0;
if (m == 0 && n == 0) {
return 0;
}
vector<vector<int>> f(m, vector<int>(n, 0));
f[0][0] = 1;
if (obstacleGrid[0][0] == 1) {
return 0;
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (obstacleGrid[i][j] == 1) {
f[i][j] = 0;
} else {
// whenever available
if (i > 0) {
f[i][j] += f[i - 1][j];
}
if (j > 0) {
f[i][j] += f[i][j - 1];
}
}
}
}
return f[m - 1][n - 1];
}
};
// Optimized using a rolling array or single row dp array instead of m x n.
class Solution {
public int uniquePathsWithObstacles(int[][] a) {
int m = a.length;
int n = a[0].length;
int dp[] = new int[n];
dp[0] = 1;
//T[i][j] = T[i-1][j] + T[i][j-1]
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(a[i][j] == 1){
dp[j] = 0;
}else if(j > 0){
dp[j] += dp[j-1];
}
}
}
return dp[n-1];
}
}
Paint House¶
- DP last step: considering the optimal solution. The last paint must be one of the three colors and the paint cost is minimum.
- State: we can try to name
f[i]the minimum cost of painting the firstihouses,i = 0, 1, ... i-1. However, we cannot know what color could be used for the last house. - Change the state to:
f[i][k]is the minium cost of painting the firstihouses and thei-1th element is painted as colork. This way, we can choose the last paint based on this piece of information. - The state transition fomular: f[i][k] = f[i - 1][\ell]_{\ell != k} + costs[i - 1][k]
- The result is minimum of the: f[i][0],\ f[i][1],\ f[i][2]
class Solution {
public:
int minCost(vector<vector<int>>& costs) {
int m = costs.size();
int f[m+1][3];
/* state: f[i][0] paint i house and the last (i - 1) house is red *
/* initial value, paint 0 house cost 0 */
for (int j = 0; j < 3; j++)
f[0][j] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 0; j < 3; j++) { // current color
f[i][j] = INT_MAX;
for (int k = 0; k < 3; k++) { // painted color
/* cannot paint same color for neighbor house */
if (j == k)
continue;
// ith (index with i - 1) house is painted with color j
if (f[i][j] > f[i - 1][k] + costs[i - 1][j])
f[i][j] = f[i - 1][k] + costs[i - 1][j];
//f[i][j] = min(f[i - 1][k] + costs[i - 1][j], f[i][j]);
}
}
}
return min(min(f[m][0], f[m][1]), f[m][2]);
}
};
Decode Ways¶
4 Ingredients
-
Last step:
A_0, A_1, A_2, ..., A_n-3, [A_n-2, A_n-1] A_0, A_1, A_2, ..., A_n-3, A_n-2, [A_n-1] -
State:
f[n]: decode ways of firstnletters. - Smaller problem:
f[n] = f[n - 1] + f[n - 2] | A_n-2,A_n-1decodable. - Init:
f[0] = 1
Note
Again the idea in this solution is to update the f[i][j] on demand, a technique that broadly used in 2-d coordinate based DP problems such as Bomb Enemy, Unique Paths II, and Minimum Path Sum.
class Solution {
public:
int numDecodings(string s) {
int n = s.length();
int f[n + 1] = {0};
if (n == 0)
return 0;
f[0] = 1;
for (int i = 1; i <= n; i++) {
int t = s[i - 1] - '0';
if (t > 0 && t <= 9) {
f[i] += f[i - 1];
}
if (i > 1){
int q = (s[i - 2] - '0') * 10 + t;
if (q >= 10 && q <= 26) {
f[i] += f[i - 2];
}
}
}
return f[n];
}
};
class Solution {
public:
int numDecodings(string s) {
if (!s.size() || s.front() == '0') return 0;
// r2: decode ways of s[0, i-2] , r1: decode ways of s[0, i-1]
int r1 = 1, r2 = 1;
// think it as a coordinate bases, not sequence based dp
for (int i = 1; i < s.size(); i++) {
// last char in s[0, i] is 0, cannot decode
if (s[i] == '0') r1 = 0;
// two-digit letter, add r2 to r1, r2 get the previous r1
if (s[i - 1] == '1' || s[i - 1] == '2' && s[i] <= '6') {
r1 = r2 + r1;
r2 = r1 - r2;
} else { // one-digit letter, r2 get the previous r1
r2 = r1;
}
}
return r1;
}
};
Longest Increasing Continuous Subsequence¶
4 ingredients:
- Last step, last element
a[n-1]could be in the result or not in the result. - subproblem, suppose we have the LICS of the first
n - 1elements. represented asf[n-1]. - base case and boundary condition, when no char in the string:
f[0] = 1. An empty string has LICS length of 1. - order of calculation, calculate small index first.
Not a leetcode
The problem is not a leetcode problem, the original problem ask for sequences that could be increase or decrease.
Using index in DP problems
Avoid using both index i - 1 and i + 1 in a loop invariance, otherwise you'll have problems in keeping the loop invariance. Compare the following.
for (int i = n - 1; i >= 0; i--) {
f[i] = 1;
if (i < n - 1 && i > 0 && A[i - 1] > A[i]) {
f[i] = f[i + 1] + 1;
}
res2 = max(res2, f[i]);
}
for (int i = n - 1; i >= 0; i--) {
f[i] = 1;
if (i < n - 1 && A[i] > A[i + 1]) {
f[i] = f[i + 1] + 1;
}
res2 = max(res2, f[i]);
}
for (int i = 0; i < n; i++) {
f[i] = 1;
if (i > 0 && A[i - 1] > A[i]) {
f[i] = f[i - 1] + 1;
}
res2 = max(res2, f[i]);
}
class Solution {
public:
int longestIncreasingContinuousSubsequence(vector<int>& A) {
// Write your code here
int n = A.size();
int f[n];
int res1 = 0;
int res2 = 0;
for (int i = 0; i < n; i++) {
f[i] = 1;
if (i > 0 && A[i - 1] < A[i]) {
f[i] = f[i - 1] + 1;
}
res1 = max(res1, f[i]);
}
for (int i = n - 1; i >= 0; i--) {
f[i] = 1;
if (i < n - 1 && A[i] > A[i + 1]) {
f[i] = f[i + 1] + 1;
}
res2 = max(res2, f[i]);
}
return max(res1, res2);
}
};
Here we don't have to explicitly wirte f[i] = max(1, f[i - 1] + 1), since we have the condition A[i - 1] < A[i], we know the A[i] will be added to the f[i], hence simply update f[i] = f[i - 1] + 1 directly.
Minimum Path Sum¶
- This is coordinate based DP. We need to have
f[i][j]to keep the minimum path sum to thegrid[i][j]. - Calculate
f[i][j]from top to down and from left to right for each row. Space can be optimized. - Notice we can do the init and first row and first column in nested loops, do not need use multiple for loops.
class Solution {
public:
int minPathSum(vector<vector<int> > &grid) {
int m = grid.size();
int n = grid[0].size();
if (m == 0 || n == 0)
return 0;
int f[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 && j == 0) {
f[i][j] = grid[i][j];
}
if (i == 0 && j > 0) {
f[i][j] = f[i][j - 1] + grid[i][j];
}
if (j == 0 && i > 0) {
f[i][j] = f[i - 1][j] + grid[i][j];
}
if (i > 0 && j > 0) {
f[i][j] = min(f[i - 1][j], f[i][j - 1]) + grid[i][j];
}
}
}
return f[m - 1][n - 1];
}
};
class Solution {
public:
int minPathSum(vector<vector<int> > &grid) {
int m = grid.size();
int n = grid[0].size();
if (m == 0 || n == 0)
return 0;
int f[2][n]; /* only two rows of status */
int prev = 1;
int curr = 1;
for (int i = 0; i < m; i++) {
// rolling the f array when move to a new row
prev = curr;
curr = 1 - curr;
for (int j = 0; j < n; j++) {
f[curr][j] = grid[i][j];
if (i == 0 && j > 0) {
f[i][j] += f[i][j - 1];
}
if (j == 0 && i > 0) {
f[curr][j] += f[prev][j];
}
if (i > 0 && j > 0) {
f[curr][j] += min(f[prev][j], f[curr][j - 1]);
}
}
}
return f[curr][n - 1];
}
};
Note
- 在处理二维坐标型DP问题的时候,对于第一行或者第一列的计算我们可以把它放到loop中。但是要加一个条件。 这个条件就是
if (i > 0), 这个条件保证了在更新数组值的时候下标不会越界。并且很好的诠释了我们的动机(就是对于第一行第一列仅仅是初始化)。 - 对于1中提到的trick,另外一个好处就是对于第一行或者第一列条件判断的时候,这里还有一个技巧就是先把自身的‘性质’或者‘值’加上, 如果有上一行我们再去加上一行的‘性质’或‘值’。这里需要逆向思维.
- 在多种情况需要分开讨论的时候我们可以先‘一票否决’最明显情况,然后讨论剩下的情况。
Bomb Enemy¶
- Breakdown the problem into smaller (simpler) problems.
- Take the special steps (i.e. different properties of the cell) as normal ones in the loop, deal with the special step when doing the calculation.
class Solution {
public:
int maxKilledEnemies(vector<vector<char>>& grid) {
int m = grid.size();
if (m == 0) return 0;
int n = grid[0].size();
if (n == 0) return 0;
int f[m][n];
int res[m][n];
int ret = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
res[i][j] = 0;
}
}
/* up */
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
f[i][j] = 0;
if (grid[i][j] == 'W') {
f[i][j] = 0;
} else {
if (grid[i][j] == 'E') {
f[i][j] = 1;
}
if (i > 0) {
f[i][j] += f[i - 1][j];
}
}
res[i][j] += f[i][j];
}
}
/* down */
for (int i = m - 1; i >= 0; i--) {
for (int j = 0; j < n; j++) {
f[i][j] = 0;
if (grid[i][j] == 'W') {
f[i][j] = 0;
} else {
if (grid[i][j] == 'E') {
f[i][j] = 1;
}
if (i < m - 1) {
f[i][j] += f[i + 1][j];
}
}
res[i][j] += f[i][j];
}
}
/* left */
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
f[i][j] = 0;
if (grid[i][j] == 'W') {
f[i][j] = 0;
} else {
if (grid[i][j] == 'E') {
f[i][j] = 1;
}
if (j > 0) {
f[i][j] += f[i][j - 1];
}
}
res[i][j] += f[i][j];
}
}
/* right */
for (int i = 0; i < m; i++) {
for (int j = n - 1; j >= 0; j--) {
f[i][j] = 0;
if (grid[i][j] == 'W') {
f[i][j] = 0;
} else {
if (grid[i][j] == 'E') {
f[i][j] = 1;
}
if (j < n - 1) {
f[i][j] += f[i][j + 1];
}
}
res[i][j] += f[i][j];
}
}
/* calculate resutls */
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '0')
if (res[i][j] > ret)
ret = res[i][j];
}
}
return ret;
}
};
Counting Bits¶
- Notice you can use the trick that
i >> 1 == i / 2to construct the subproblem
| i | count 1 bits |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 6 | 2 |
| 12 | 2 |
| 25 | 3 |
| 50 | 3 |
class Solution {
public:
vector<int> countBits(int num) {
vector<int> f(num + 1, 0);
if (num == 0) {
return f;
}
for (int i = 1; i <= num; i++) {
f[i] = f[i >> 1] + (i % 2);
}
return f;
}
};
Lecture 3 Dynamic Programming on Sequences¶
| Problem | Category |
|---|---|
| Paint House II | 序列型+状态 |
| House Robber | 序列型+状态 |
| House Robber II | 序列型+状态 |
| Best Time to Buy and Sell Stock | |
| Best Time to Buy and Sell Stock II | |
| Best Time to Buy and Sell Stock III | 序列型+状态 |
| Best Time to Buy and Sell Stock IV | 序列型+状态 |
| Longest Increasing Subsequence | 序列型 |
| Russian Doll Envelopes |
序列型动态规划¶
给定一个序列
- 动态规划方程
f[i]中的下标i表示前i个元素a[0], a[1], ..., a[i-1]的某种性质- 坐标型的
f[i]表示以a[i]为结尾的某种性质
- 坐标型的
- 初始化中,
f[0]表示空序列的性质- 坐标型动态规划的初始条件
f[0]就是指以a[0]为结尾的子序列的性质
- 坐标型动态规划的初始条件
Paint House II¶
- the solution could be the same as the first version, but it is O(n\cdot k^2). how to make it O(n\cdot k)?
- By analyzing the state transition equation, we observed that we want to find a minimum value of a set of numbers except one for each house. Put it in English, the min cost to paint
i - 1th house with colork, we want to have the min cost of painting all previousi - 1houses and thei-1th house cannot be painted as colork.
f[i][1] = min{f[i-1][2] + cost[i-1][1], f[i-1][3] + cost[i-1][1], ..., f[i-1][K] + cost[i-1][1]}
f[i][2] = min{f[i-1][1] + cost[i-1][2], f[i-1][3] + cost[i-1][2], ..., f[i-1][K] + cost[i-1][2]}
...
f[i][K] = min{f[i-1][1] + cost[i-1][K], f[i-1][2] + cost[i-1][K], ..., f[i-1][K-1] + cost[i-1][K]}
- We could optimize the solution upon this. Basically, we can maintain the first two minimum value of the set
f[i-1][1], f[i-1][2], f[i-1][3], ..., f[i-1][K],min1andmin2and their indexj1andj2.- There are two cases, the first case is the house
i-1is painted with the same color correspoinding to the minimum value. in this case, we cannot chose to paint it with the color corresponding to the minimum cost, we can update the state using the second minimum. - The second case is that we paint the i-1th house with color other than the color corresponding to the minimum cost to pain, we can update using the minimum value.
- There are two cases, the first case is the house
class Solution {
public:
/**
* @param costs n x k cost matrix
* @return an integer, the minimum cost to paint all houses
*/
int minCostII(vector<vector<int>>& costs) {
int m = costs.size();
if (m == 0) return 0;
int k = costs[0].size();
if (k == 0) return 0;
int f[m + 1][k];
int min1;
int min2;
int j1 = 0, j2 = 0;
/* init, 0 house cost nothing. */
for (int j = 0; j < k; j++)
f[0][j] = 0;
for (int i = 1; i <= m; i++) {
min1 = min2 = INT_MAX;
/* from all the colors, find the min1 and min2 */
for (int j = 0; j < k; j++) {
/* get the min1 and min2 first */
if (f[i - 1][j] < min1) {
min2 = min1;
j2 = j1;
min1 = f[i - 1][j];
j1 = j;
} else if (f[i - 1][j] < min2) {
min2 = f[i - 1][j];
j2 = j;
}
}
/* update the states based on the min1 and min2 */
for (int j = 0; j < k; j++) {
if (j != j1) {
f[i][j] = f[i - 1][j1] + costs[i - 1][j];
} else {
f[i][j] = f[i - 1][j2] + costs[i - 1][j];
}
}
}
int res = INT_MAX;
for (int j = 0; j < k; j++) {
if (f[m][j] < res)
res = f[m][j];
}
return res;
}
};
class Solution {
public:
int minCostII(vector<vector<int>>& costs) {
int n = costs.size();
int k = n > 0 ? costs[0].size() : 0;
if (n == 0 && k == 0)
return 0;
if (n == 1 && k == 1)
return costs[0][0];
vector<vector<int>> f(n + 1, vector<int>(k, 0));
for (int i = 0; i < k; i++) {
f[0][i] = 0; // 0 cost for 0 paint
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j < k; j++) {
f[i][j] = INT_MAX;
for (int c = 0; c < k; c++) {
if (j == c) {
continue;
}
if (f[i][j] > f[i - 1][c] + costs[i - 1][j]) {
f[i][j] = f[i - 1][c] + costs[i - 1][j];
}
}
}
}
int res = INT_MAX;
for (int i = 0; i < k; i++) {
if (f[n][i] < res)
res = f[n][i];
}
return res;
}
};
House Robber¶
- Start with the last step. The last house could be either robbed or not.
- If the last house
a[i-1]is robbed, then we cannot roba[i-2]. we havef[i] = f[i-2] + a[i-1]. - If the last house
a[i-1]is not robbed, then we can roba[i-2]. Alternatively, we can skip it to roba[i-3]. We havef[i] = f[n-1], in which thisf[n-1]could not let us know whethera[i-2]is robbed or not.
- If the last house
- We add the state of
a[i-1]to the state transition equation. Thus we have:f[i][0]represent "the maximum money for robbing the firstihouses and the last house hasn't been robbed."f[i][1]represent "the maximum money for robbing the firstihouses and the last house has been robbed."
- state transition equations:
f[i][0] = max(f[i-1][0], f[i-1][1]) f[i][1] = f[i-1][0] + a[i-1]
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if (n == 0)
return 0;
int f[n + 1][2] = {0};
for (int i = 1; i <= n; i++) {
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + nums[i - 1];
}
return max(f[n][0], f[n][1]);
}
};
class Solution {
public:
long long houseRobber(vector<int> A) {
int n = A.size();
if (n == 0) return 0;
long long f[n+1];
/* init */
f[0] = 0;
f[1] = A[0];
for (int i = 2; i <= n; i++) {
f[i] = max(f[i - 1], f[i - 2] + A[i - 1]);
}
return f[n];
}
};
Solution 2
yes- firstidays, robber last day,no- firstidays, not robber at last day.
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if (n == 0)
return 0;
int yes = 0, no = 0;
for (int i = 1; i <= n; i++) {
int tmp = no;
no = max(yes, no);
yes = tmp + nums[i - 1];
}
return max(yes, no);
}
};
House Robber II¶
- Following House Robber, when we try to analyze the last step, the house
i - 1depends on the housei - 2and the house0. How could we handle this? - We could enumerate two cases, and reduce the probelm to House Rober
- house
0is robbed and housei-1is not. - house
i - 1is robbed and house0is not.
- house
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if (n == 0)
return 0;
if (n == 1) // edge case to deal with
return nums[0];
vector<int> nums1(nums.begin() + 1, nums.end());
vector<int> nums2(nums.begin(), nums.end() - 1);
return max(rob_helper(nums1), rob_helper(nums2));
}
private:
int rob_helper(vector<int>& A) {
int n = A.size();
if (n == 0)
return 0;
int f[n+1] = {0};
f[0] = 0;
f[1] = A[0];
for (int i = 2; i <= n; i++) {
f[i] = max(f[i - 1], f[i - 2] + A[i - 1]);
}
return f[n];
}
};
Best Time to Buy and Sell Stock¶
- Force youself to do it by only one pass. You'll find that you need two variables to record the minimum value currently found and the maximum profit currently found.
class Solution {
public:
int maxProfit(vector<int> &prices) {
int n = prices.size();
if (n == 0)
return 0;
int min_price = INT_MAX;
int max_profit = 0;
for (int i = 0; i < n; i++) {
if (prices[i] < min_price) {
min_price = prices[i];
} else if (prices[i] - min_price > max_profit) {
max_profit = prices[i] - min_price;
}
}
return max_profit;
}
};
Best Time to Buy and Sell Stock II¶
- We can just buy and sell when ever the price is increased in a day.
- Once you can proof the day-by-day subproblem can form the solution. The solution becomes so easy.
class Solution {
public:
int maxProfit(vector<int> &prices) {
int res = 0;
for (int i = 1; i < prices.size(); i++) {
if (prices[i - 1] < prices[i])
res += prices[i] - prices[i - 1];
}
return res;
}
};
class Solution {
public:
int maxProfit(vector<int> &prices) {
int res = 0;
for (int i = 1; i < prices.size(); i++) {
res += max(prices[i] - prices[i - 1], 0)
}
return res;
}
};
Best Time to Buy and Sell Stock III¶
- We can define 5 stages and write state transition equations based on it.
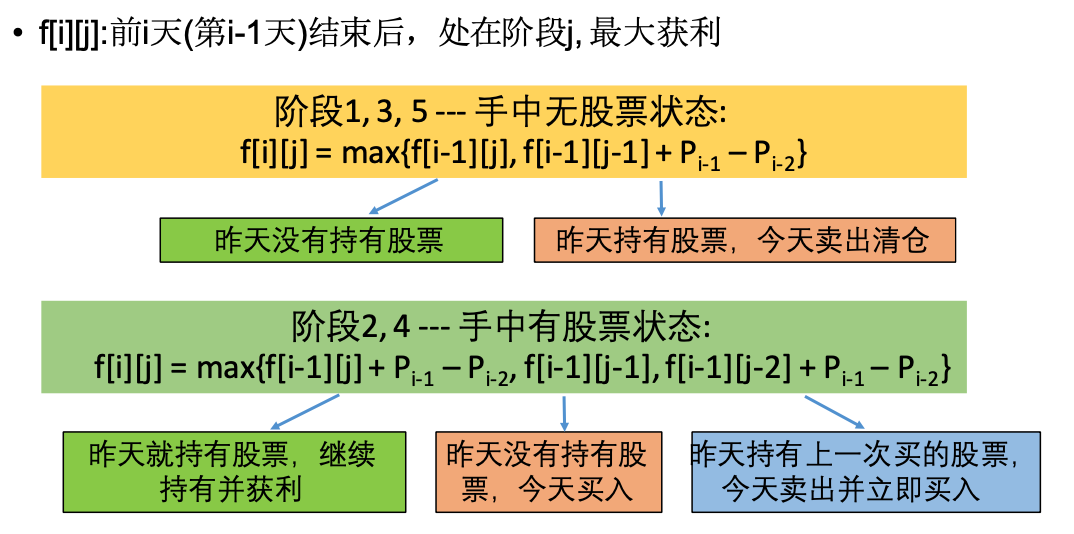
class Solution {
public:
/**
* @param prices: Given an integer array
* @return: Maximum profit
*/
int maxProfit(vector<int> &A) {
int n = A.size();
if (n == 0) {
return 0;
}
int f[n+1][6];
/* init */
f[0][1] = 0;
f[0][2] = f[0][3] = f[0][4] = f[0][5] = INT_MIN;
for (int i = 1; i <= n; i++) {
// stage 1, 3, 5:
// f[i][j] = max{f[i - 1][j], f[i - 1][j - 1] + A[i - 1] - A[i - 2]}
for (int j = 1; j <= 5; j += 2) {
f[i][j] = f[i - 1][j];
if (i > 1 && j > 1 && f[i - 1][j - 1] != INT_MIN) {
f[i][j] = max(f[i][j], f[i - 1][j - 1] + A[i - 1] - A[i - 2]);
}
}
// stage 2, 4:
// f[i][j] = max{f[i - 1][j] + A[i - 1] - A[i - 2], f[i - 1][j - 1], f[i - 1][j - 2] + A[i - 1] - A[i - 2]}
for (int j = 2; j < 5; j += 2) {
f[i][j] = f[i - 1][j - 1];
if (i > 1 && f[i - 1][j] != INT_MIN) {
f[i][j] = max(f[i][j], f[i - 1][j] + A[i - 1] - A[i - 2]);
}
if (i > 1 && j > 2 && f[i - 1][j - 2] != INT_MIN) {
f[i][j] = max(f[i][j], f[i - 1][j - 2] + A[i - 1] - A[i - 2]);
}
}
}
return max(f[n][1], max(f[n][3], f[n][5]));
}
};
Best Time to Buy and Sell Stock IV¶
- If
kis larger thenn/2, it is equivalent to the II. - This is a generalized solution from Best Time to Buy and Sell Stock III.
class Solution {
public:
int maxProfit(int K, vector<int> &A) {
int n = A.size();
if (n == 0) {
return 0;
}
int f[n+1][2 * K + 1 + 1];
/* special case need to take care of */
if (K > (n / 2)) {
int res = 0;
for (int i = 0; i + 1 < n; i++) {
if (A[i + 1] - A[i] > 0) {
res += A[i + 1] - A[i];
}
}
return res;
}
/* init */
f[0][1] = 0;
for (int k = 2; k <= 2 * K + 1; k++) {
f[0][k] = INT_MIN;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= 2 * K + 1; j += 2) {
f[i][j] = f[i - 1][j];
if (i > 1 && j > 1 && f[i - 1][j - 1] != INT_MIN) {
f[i][j] = max(f[i][j], f[i - 1][j - 1] + A[i - 1] - A[i - 2]);
}
}
for (int j = 2; j < 2 * K + 1; j += 2) {
f[i][j] = f[i - 1][j - 1];
if (i > 1 && f[i - 1][j] != INT_MIN) {
f[i][j] = max(f[i][j], f[i - 1][j] + A[i - 1] - A[i - 2]);
}
if (i > 1 && j > 2 && f[i - 1][j - 2] != INT_MIN) {
f[i][j] = max(f[i][j], f[i - 1][j - 2] + A[i - 1] - A[i - 2]);
}
}
}
int res = INT_MIN;
for (int j = 1; j <= 2 * K + 1; j += 2 ) {
if (f[n][j] > res)
res = f[n][j];
}
return res;
}
};
Longest Increasing Subsequence¶
- Comparing to the problem Longest Increasing Continuous Subsequence. If the subsequence is not continuous. we have to enumerate each of the previous element before
A[j].
Solution 2 DP with binary search O(nlogn)
- To reduce the complexity, we can try to find if there is any redundant work we have been done. or some how we could use some order information to avoid some of the calculation.
- Focus on the real meaning of longest Increasing Subsequence. In fact, you are looking for the smallest value before
A[i]that leads to the longest Increasing Subsequence so far. - use the state
f[i]to record the LIS of the arrayA[0], ... A[i -1]. If we are atf[j], j > i, we are looking for the largestf[i]value that have the smallestA[i].
Solution 3 DP with binary search refactored
- In observing the fact that we can use extra space to keep the "minimum elements see so far from nums that is the last element of LIS for the different length of such LISes".
- Different from the regular DP solution, our extra space b is storing element from nums, and the element stored in b are not necessary in order.
- The index i of elements in b related to the length of a LIS whose last element is
a[i]. specifically,i + 1 = length(LIS).
Solution 4 C++ using lower_bound
- We can use the
lower_boundto replace the binary search routine in the above solution.
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
if (n == 0)
return 0;
int res = 0;
int f[n] = {0};
for (int j = 0; j < n; j++) {
/* case 1: a[j] is the subsequence */
f[j] = 1;
/* case 2: LIS from a[0],...a[i] plus a[j] */
for (int i = 0; i < j; i++) {
if (nums[i] < nums[j] && f[i] + 1 > f[j])
f[j] = f[i] + 1;
}
res = max(res, f[j]);
}
return res;
}
};
class Solution {
public:
int longestIncreasingSubsequence(vector<int> nums) {
int n = nums.size();
if (n == 0)
return 0;
//int f[n];
// b[i]: when f value is i, smallest a value (ending value)
int b[n + 1];
int top = 0;
b[0] = INT_MIN;
// O(n)
for (int i = 0; i < n; i++) {
// b[0] ~ b[top]
// last value b[j] which is smaller than A[i]
int start = 0, end = top;
int mid;
int j;
// O(lgn)
while (start <= end) {
mid = start + (end - start) / 2;
if (b[mid] < nums[i]) {
j = mid;
start = mid + 1;
} else {
end = mid - 1;
}
}
// b[i]: length is j (f value is j), smallest ending value.
// A[i] is after it.
// f[i] = j + 1
// b[j + 1]: length is (j + 1), smallest ending value.
// A[i]
// B[j + 1] >= A[i]
b[j + 1] = nums[i];
if (j + 1 > top) {
top = j + 1;
}
}
// b[top] stores the smallest ending value for an LIS
return top;
}
};
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> b;
for (int i = 0; i < nums.size(); ++i) {
int begin = 0, end = b.size();
while (begin != end) {
int mid = begin + (end - begin) / 2;
if (b[mid] < nums[i]) {
begin = mid + 1;
} else {
end = mid;
}
}
if (begin == b.size()) // nums[i] greater than all element in b
b.push_back(nums[i]);
else // begin point to next element no less than the target nums[i].
b[begin] = nums[i];
}
return b.size();
}
};
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> b;
for (auto a : nums) {
auto it = lower_bound(b.begin(), b.end(), a);
if (it == b.end()) b.push_back(a);
else *it = a;
}
return b.size();
}
};
Russian Doll Envelopes¶
- Sort the vector in ascending order and identify the subproblem, apply DP.
- notice the sort is ascending, not descending.
- For the
O(nlogn)solution, think of how to optimize the longest increasing subsequence for one dimension when the envelopes are sorted properly. -
We use
b[k]to record the smallestA[i]value that have length ofklongest increasing subsequence. The reason behind this can be illustrated by the following example, wheni = 1, we can forgetA[0] = 5, because what ever LISA[0] = 5can contribute to the LIS,A[1] = 2will be able to contribute.A[i] 5, 2, 3, 1, 4 f[i] 1, 1, 2, 2, 3 b[k] 5 (|k| = 1, i = 0) b[k] 2 (|k| = 1, i = 1) b[k] 2, 3 (|k| = 2, i = 2) b[k] 2, 1 (|k| = 2, i = 3) b[k] 2, 1, 4 (|k| = 2, i = 4) -
In iterating of
A[i]we binary search to find the smaller value thanA[i]inb[k]so far that this smaller value combined withA[i]will form a new LIS. To keep the loop invariant, we need to changeb[k]by either modify the existing value inb[k]or add a new value to the end.
class Solution {
public:
int maxEnvelopes(vector<vector<int>>& envelopes) {
int n = envelopes.size();
int f[n];
int res = 0;
sort(envelopes.begin(), envelopes.end(), [](vector<int>& a, vector<int>& b){
if (a[0]== b[0]) {
return a[1] < b[1];
} else {
return a[0] < b[0];
}
});
for (int i = 0; i < n; ++i) {
f[i] = 1;
for (int j = 0; j < i; ++j) {
if (envelopes[j][0] < envelopes[i][0] && envelopes[j][0] < envelopes[i][0]) {
f[i] = max(f[i], f[j] + 1);
}
}
res = max(res, f[i]);
}
return res;
}
};
class Solution {
public:
int maxEnvelopes(vector<pair<int, int>>& envelopes) {
int n = envelopes.size();
if (n == 0)
return 0;
vector<int> f;
sort(envelopes.begin(), envelopes.end(), [](const pair<int, int> a, const pair<int, int> b) {
if (a.first == b.first) {
return a.second > b.second;
} else {
return a.first < b.first;
}
});
for (int i = 0; i < n; ++i) {
int t = envelopes[i].second;
int begin = 0, end = f.size(); // f start with empty
// when i = 0, the binary search will not happen, first value will
// be added to f before binary search on it.
while (begin < end) {
int mid = begin + (end - begin) / 2;
if (f[mid] < t) {
begin = mid + 1;
} else {
end = mid;
}
}
if (begin == f.size()) {
f.push_back(t);
} else {
f[begin] = t; // index to f is related to the result
}
}
return f.size();
}
};
Lecture 4¶
| Problem | category |
|---|---|
| Perfect Squares | 划分型/序列型 |
| Palindrome Partitioning II | 划分型 |
| Copy Books | 划分型 |
| Coins in A Line | 博弈型 |
| Backpack | 背包型 |
| Backpack V | 背包型 |
| Backpack VI | 背包型 |
Perfect Squares¶
- f[i] = \min_{1 \le j^2 \le i}(f[i - j^2] + 1) 整体思想就是枚举
j. - 本题分析时像划分型但程序写起来像序列型。还是从最后一步入手。设最后一个是j^2.
- 整体思想就是枚举最后一步
j. 注意初始化f[i].j*j可以是i, 这个正好对应了极端情况 就是i只由j*j组成. - if condition 无需检查
f[i - j*j]是否为INT_MAX. 因为这里比i小的i - j*j总是可以由完全平方数1组成。相比较题目 Coin Change 这道题,这一步可能性检查必不可少,因为在 Coin Change 中某一面值不一定能被兑换成给定面值的硬币。我们用无穷大来标记。
class Solution {
public:
int numSquares(int n) {
if (n == 0)
return 0;
int f[n+1] = {0};
f[0] = 0;
for (int i = 1; i <= n; i++) {
f[i] = INT_MAX;
for (int j = 1; j * j <= i; j++) {
if (f[i - j*j] + 1 < f[i]) {
f[i] = f[i - j*j] + 1;
}
}
}
return f[n];
}
};
class Solution:
def numSquares(self, n: int) -> int:
if n == 0:
return 0
f = [0] * (n + 1)
for i in range(1, n + 1):
f[i] = float('inf')
for j in range(1, int(sqrt(i)) + 1):
if f[i] > f[i - j*j] + 1:
f[i] = f[i - j*j] + 1
return f[n]
Palindrome Partitioning II¶
- Consider the last palindrome
s[j, ..., i - 1],f[i]represent the minimum number of partitions of firsticharacters. - State transition equation: f[i] = \min_{0 \le j \lt i}(f[j]+1 | (s[j],..., s[i-1]) \text{ is palindrome})
- To know the substr
s[j, ... i-1]is a palindrome or not, we can first find and record all the panlidrome substring inisPalin[i][j], each element of which represents whether substrs[i, ..., j]is a palindrome or not.
class Solution {
public:
int minCut(string s) {
int n = s.length();
if (n == 0)
return 0;
int isPalin[n][n];
int f[n + 1];
f[0] = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
isPalin[i][j] = 0;
}
}
/* calculate palindrome */
for (int t = 0; t < n; t++) {
/* odd case */
int i = t;
int j = t;
while (i >= 0 && j < n && s[i] == s[j]) {
isPalin[i][j] = 1;
i--;
j++;
}
/* even case */
i = t;
j = t + 1;
while (i >= 0 && j < n && s[i] == s[j]) {
isPalin[i][j] = 1;
i--;
j++;
}
}
/* calculate the states */
for (int i = 1; i <= n; i++) {
f[i] = INT_MAX;
for (int j = 0; j < i; j++) {
if (isPalin[j][i - 1]) {
f[i] = min(f[i], f[j] + 1);
}
}
}
return f[n] - 1;
}
};
public class Solution {
/**
* @param s a string
* @ f[i], minmum cut of s[0],...s[i - 1]
* e.g.
* a a b a a
* j=0 1 2 3 4
*i=0 a 1 1 0
* 1 a 1 0
* 2 b 1 0
* 3 a 1 0
* 4 a 1
*
* when calculate isPalin[i][j], we need to know isPalin[i + 1][j + 1].
* Cannot calculate from i = 0, 1, ... have to go from i = n - 1, n - 2, ... 1, 0
* last step: s[j],...s[i - 1]
* f[i] = f[j] + 1 | s[j], ... s[i - 1] is palindrome
*/
public int minCut(String ss) {
char[] s = ss.toCharArray();
int n = s.length;
if (n == 0)
return 0;
boolean[][] isPalin = new boolean[n][n];
int[] f = new int[n + 1];
f[0] = -1;
for (int i = 0; i < n; i++) {
isPalin[i][i] = true;
if (i + 1 < n) {
isPalin[i][i + 1] = s[i] == s[i + 1];
}
}
for (int i = n - 3; i >= 0; i--) {
for (int j = i + 2; j < n; j++) {
isPalin[i][j] = isPalin[i + 1][j - 1] && s[i] == s[j];
}
}
/* calculate the states */
for (int i = 1; i <= n; i++) {
f[i] = i - 1;
for (int j = 0; j < i; j++) {
if (isPalin[j][i - 1]) {
f[i] = Math.min(f[i], f[j] + 1);
}
}
}
return f[n];
}
};
Warning
这个方法C++不能通过Leetcode和lintcode,主要是对于很长的string,isPalin会很大。类似于 Best Time to Buy and Sell Stock IV 中如果k很大的时候。Java版本则可以。
Note
技巧:在循环中需要某个性质,而这个性质又是可以很容易计算和记录 (isPalin) 我们就采用先计算所有并记录,在loop中去直接访问符合条件的结果即可。
Copy Books¶
Coins in A Line¶
- 要有先手“必胜”和“必败”的概念。简单来讲就是当前先手面对当前局势如果有一招能使下轮先手必败 那么当前选手就必胜。如果当前选手面对当前局势下所有招数都会使得下轮先手必胜,那么当前选手必败。
f[i]表示当前选手必胜(True)或必败(False).- State transition equation: f[i] = f[i - 1] == \text{false}\ OR\ f[i - 2] == \text{false}
- 此题注意初始条件和必胜和必败的概念就不会有什么差错。

class Solution {
public:
bool firstWillWin(int n) {
if (n == 0)
return false;
bool f[n];
f[0] = false;
for (int i = 1; i <= 2; i++) {
f[i] = true;
}
for (int i = 3; i <= n; i++) {
f[i] = (f[i - 1] == false) || (f[i - 2] == false);
}
return f[n];
}
};
// You can actualy found the pattern if you have written several states. f[i] = i % 3
// 0 1 2 3 4 5 6 7 8 9 10
// F T T F T T F T T F T
class Solution {
public:
bool firstWillWin(int n) {
return n % 3;
}
};
Backpack¶
- Give
nitems with sizeA[i]and backpack size:M. Find the max total size that can fit in the backpack. - We can reduce the size of f to two rolls. We can even reduce it to just one dimention. same technique can also be used in Backpack II and Backpack V.
class Solution {
public:
int backPack(int m, vector<int> A) {
int n = A.size();
if (n == 0)
return 0;
bool f[n + 1][m + 1];
/* init */
f[0][0] = true;
for (int j = 1; j <= m; j++) {
f[0][j] = false;
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j]; /* must first init f[i][j] */
if (j >= A[i - 1]) {
f[i][j] = f[i][j] || f[i - 1][j - A[i - 1]];
//f[i][j] = f[i - 1][j] || f[i - 1][j - A[i - 1]]; /* this is wrong */
}
}
}
for (int j = m; j >= 0; j--) {
if (f[n][j] == true)
return j;
}
return 0;
}
};
class Solution {
public:
int backPack(int m, vector<int> A) {
int n = A.size();
if (n == 0)
return 0;
bool f[m + 1];
/* init */
f[0] = true;
for (int j = 1; j <= m; j++) {
f[j] = false;
}
for (int i = 1; i <= n; i++) {
for (int j = m; j >= 0; j--) {
if (j >= A[i - 1]) {
f[j] = f[j] || f[j - A[i - 1]];
}
}
}
for (int j = m; j >= 0; j--) {
if (f[j] == true)
return j;
}
return 0;
}
};
Backpack V¶
- This problem could follow the analysis from Backpack.
- Instead of memorize the boolean value whether first
iitems can fill the weightw. We record inf[i][w]the total number of possible fills of the weightwby firstiitems. - We need to initialize the state
f[i][j]first then to update it.
class Solution {
public:
int backPackV(vector<int>& nums, int T) {
int n = nums.size();
if (n == 0) {
return 0;
}
int f[n + 1][T + 1];
f[0][0] = 1;
for (int j = 1; j <= T; j++) {
f[0][j] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= T; j++) {
f[i][j] = f[i - 1][j];
if (j >= nums[i - 1]) {
f[i][j] += f[i - 1][j - nums[i - 1]];
}
}
}
return f[n][T];
}
};
class Solution {
public:
int backPackV(vector<int>& nums, int T) {
int n = nums.size();
if (n == 0) {
return 0;
}
int f[T + 1];
f[0] = 1;
for (int j = 1; j <= T; j++) {
f[j] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = T; j >= 0; j--) {
//f[j] = f[j - A[i - 1]] ==> f'[j]
if (j >= nums[i - 1]) {
// f'[j]
// cover old f[j]
f[j] += f[j - nums[i - 1]];
}
}
}
return f[T];
}
};
Backpack VI¶
- 这道题等同于Leetcode里 Combinations Sum IV
- 这里可以随便取,似乎题目变得无法下手,考虑“最后一步”这个技巧不能用了,因为最后一步可以是任意一个了。
- 但仍然可以用子问题来考虑。先不管最后一步是哪一个,最后一步之前的相加的总和一定是
Target - x. 这样就转化成一个子问题可以用DP来做。 具体做法我们可以对于每一个小于“总承重”的重量进行枚举最后一步x. 可能的x是A[0], ..., A[i - 1]中任意一个. - Must initialize
f[i] = 0. Because some of the state won't be updated (indicate they are not possible to be fill).
class Solution {
public:
int backPackVI(vector<int>& nums, int T) {
int n = nums.size();
if (n == 0) {
return 0;
}
int f[T + 1];
f[0] = 1;
/* for each sub problem */
for (int i = 1; i <= T; i++) {
f[i] = 0;
/* enumerate the last step */
for (int j = 0; j < n; j++) {
if (i >= nums[j]) {
f[i] += f[i - nums[j]];
}
}
}
return f[T];
}
};
// f[i]: 存多少种方式
// pi[i]: 如果 f[i] >= 1, 最后一个数字可以是pi[i]
class Solution {
public:
int backPackVI(vector<int>& nums, int T) {
int n = nums.size();
if (n == 0) {
return 0;
}
int f[T + 1];
/* pi[i]: 如果i可拼出(f[i] >= 1), 最后一个是pi[i] */
int pi[T + 1];
f[0] = 1;
for (int i = 1; i <= T; i++) {
f[i] = 0;
for (int j = 0; j < n; j++) {
if (i >= nums[j]) {
f[i] += f[i - nums[j]];
/* 最后一个是nums[j]的可拼出i */
if (f[i - nums[j]] > 0) {
/* 纪录下来 */
pi[i] = nums[j];
}
}
}
}
if (f[T] > 0) {
int i = T;
cout << i << "=" << endl;
while (i != 0) {
// sum is i now;
// last number is pi[i]
// previuos sum is i - pi[i]
cout << pi[i] << endl;
i -= pi[i];
}
}
return f[T];
}
};
Summary Dynamic Programming Types¶
划分型动态规划特点¶
- 给定长度为N的序列或字符串,要求划分成若干段
- 段数不限,或指定K段
- 每一段满足一定的性质
- 类似于序列型动态规划,但是通常要加上段数信息
- 类似于序列型动态规划,但是通常要加上段数信息
- 一般用
f[i][j]记录前i个元素(元素0~i-1)分成j段的性质,如最小代价 - 把状态
f[i]或f[i][j]初始化为极大值或极小值。一方面,这样有利于在更新状态时计算最 大或最小值;另一方面,在更新状态是可以通过查看子状态是否为极值来判断当前一步更新是否有意义。 典型题目:1. Perfect Squares, 全部状态都有意义,可省略检查。2. Coin Change 有些 数额是无法用给定面值的硬币兑换,更新前需检查状态是否为极致以判断当前更新是否有意义。
- 划分性动态规划总结
- 要求将一个序列或字符串划分成若干满足要求的片段
- 解决方法:最后一步/最后一段
- 枚举最后一段的起点
- 如果题目不指定段数,用 f[i] 表示前 i 个元素分段后的可行性/最值,可行性,方式数: Perfect Squares, Palindrome Partition II
- 如果题目指定段数,用 f[i][j]表示前 i 个元素分成 j 段后的可行性/最值,可行性,方式数:Copy Books
- 背包型动态规划类型
- 布尔值
- 计数
- 最值
- 单一物品
- 无限多物品
- 背包型动态规划空间优化
- 滚动数组
- 单个数组
- 背包型动态规划总结
- 背包问题的数组大小与总承重有关
- Backpack 可行性背包
- 要求不超过Target时能拼出的最大重量
- 记录前i个物品能不能拼出重量w
- Backpack V, Backpack VI, 计数型背包
- 要求有多少种方式拼出重量Target
- Backpack V:记录前i个物品有多少种方式拼出重量w
- Backpack VI:记录有多少种方式(可重复)拼出重量w
- 关键点
- 最后一步
- 最后一个背包内的物品是哪个
- 最后一个物品有没有进背包
Note
注意在loop中要先初始化f[i][j], 然后再去更新,否者如果if语句判断false的时候是没法更新f[i][j]的。例如题目:Backpack 和 Backpack V
Lecture 5¶
| Problem | Category |
|---|---|
| Backpack II | 背包型 |
| Backpack III | 背包型 |
| Coins in A Line III | 博弈型 |
| Longest Palindromic Subsequence | 区间型 |
| Burst Balloons | 区间型 |
| Scramble String | 区间型 |
Backpack II¶
Given n items with size A[i] and value V[i], and a backpack with size m. What's the maximum value can you put into the backpack?
Example
Given 4 items with size [2, 3, 5, 7] and value [1, 5, 2, 4], and a backpack with size 10. The maximum value is 9.
- 思考方式任然是从最后一个物品选还是不选,只是我们现在考虑的是价值。此时状态就不能是可行性 Backpack或者多少种了Backpack V, 我们要纪录总价值。
- State:
f[i][w]represent the value of the firstiitems that weightw. - State transition equation: f[i][w] = max(f[i - 1][w],\ f[i - 1][w - A[i - 1]] + V[i - 1] | w ≥ A[i-1] \text{且}\ f[i-1][w-A[i-1]] \neq -1)
- Initialization:
f[0][0] = 0,f[0][1] = -1, ... f[0][w] = -1.-1代表不能被拼出。
class Solution {
public:
int backPackII (vector<int> A, vector<int> V, int m) {
int n = A.szie();
if (n == 0) return 0;
int f[n + 1][m + 1];
f[0][0] = 0;
for (int j = 1; j < m; ++j) {
f[0][j] = -1;
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
f[i][j] = f[i - 1][j];
if (f[i - 1][j - A[i - 1]] != -1 && j >= A[i - 1]) {
f[i][j] = max(f[i][j], f[i - 1][j - A[i - 1]] + V[i - 1]);
}
}
}
int res = 0;
for (int j = 0; j <= m; ++j) {
if(f[n][j] != -1 && f[n][j] > res) {
res = f[n][j];
}
}
return res;
}
};
class Solution {
public:
int backPackII (vector<int> A, vector<int> V, int m) {
int n = A.szie();
if (n == 0) return 0;
int f[m + 1];
f[0] = 0;
for (int j = 1; j < m; ++j) {
f[0][j] = -1;
}
for (int i = 1; i <= n; ++i) {
for (int j = m; j >= 0; --j) {
if (f[j - A[i - 1]] != -1 && j >= A[i - 1]) {
f[j] = max(f[j], f[j - A[i - 1]] + V[i - 1]);
}
}
}
int res = 0;
for (int j = 0; j <= m; ++j) {
if(f[j] != -1 && f[j] > res) {
res = f[j];
}
}
return res;
}
};
Backpack III¶
Given n kind of items with size A[i] and value V[i]( each item has an infinite number available) and a backpack with size m. What's the maximum value can you put into the backpack?
Example
Given 4 items with size [2, 3, 5, 7] and value [1, 5, 2, 4], and a backpack with size 10. The maximum value is 15.
- We can follow the "last step" principle, assume the last item in and not in the backpack. But when we do this, we notice that the last one item could also be in the previous because we have infinite times of the item available. We cannot proceed.
- Instead of thinking the "last one" in the final answer, we can think the "last one" that has been selected. This paradigm shift enables use to tackle the problem more cleverly. We can enumerate the last type (not the last one in the final result) of items we can select.
- State:
f[i][w]: 前i种物品能够拼成重量为w的最大价值 - Transition equation: f[i][w] = \max_{k \ge 0}{f[i-1[w], f[i - 1][j - k A[i -1]] + k V[i-1]}

class Solution {
public:
int backPackIII(vector<int>& A, vector<int>& V, int m) {
int n = A.size();
if (n == 0) {
return 0;
}
int f[m + 1];
/* init */
f[0] = 0;
for (int j = 1; j <= m; j++) {
f[j] = -1;
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if (f[j - A[i - 1]] != -1 && j >= A[i - 1]) {
f[j] = max(f[j], f[j - A[i - 1]] + V[i - 1]);
}
}
}
int res = 0;
for (int j = 0; j <= m; j++) {
if (f[j] != -1 && f[j] > res) {
res = f[j];
}
}
return res;
}
};
Note
Notice the solution is identical to the Backpack II except one line (line 18), but you should notice there is a long way from Backpack II to Backpack III. See the detailed explaination of this problem in Dynamic Programming
Coins in A Line III¶
There are n coins in a line. Two players take turns to take a coin from one of the ends of the line until there are no more coins left. The player with the larger amount of money wins. Could you please decide the first player will win or lose?
-
这是一个博弈问题。看上去很难入手。要对题目认真审视。我开始的时候就没有懂得题意。下面是我的错误分析。
/***************** WRONG *************************** * 当前局面:a[i], ... a[j] * Alice = A, Bob = B, * Sa = A - B; * 先手: Alice A + a[i](a[j]) * Bob = B, * 下一轮:a[i+1], ... a[j] * Alice = A' = A + a[i], Bob = B' = B, * Sb = B - A'; * 先手:Bob B + a[i + 1] (a[j - 1]) * 后手:Alice: A'; * ... * * *** Sb = B - A - a[i] * *** Sb = -Sa - a[i] * * **************** WRONG ****************************/ -
注意这道题问的是先手是否会赢。所以应该以“先手”这个关键词出发。就是第一步。这一点明确了, 再重新分析,问题迎刃而解。
/* 注意:我们的题意是问先手是否必胜。则当考虑先手出手之前的状态 * * 当前局面:a[0], ... a[n-1] * Alice = A = 0, Bob = B = 0, * delta: Sa = A - B = 0; * 先手: Alice 取 a[i](或者a[j]), 目标是最大化A - B * A = a[i] * B = 0, * 在接下来的每轮中,Bob尽最大努力去最大化B - A * 最终:Alice 获得 A + a[i], * Bob 获得 B, * 注意:最终结果指的是“必胜”或“必败”的法则走到最后. * 必胜必败概念:先手在当前局面有一种可能性“必胜”则“必胜”,没有一种"必胜"可能性便“必败”。 * 我们想知道的是Sa = A + a[i] - B = -Sb + a[i]是否会大于0 * * 我们发现 Sa = -Sb + a[i] * 这是个子问题。子问题是相对于先手Alice来讲的,子问题可以看做每次轮到Alice的局面(先手), Alice 的问题规模都变小了。 * State: f[i][j] = Alice面对局面a[i], ... a[j]时能得到的最大的于对手的数值差。 * Equation: f[i][j] = max(a[i] - f[i+1][j], a[j] - f[i][j-1]) * Init: f[0][0] = 0; * f[i][i] = a[i]; * 区间型,写code应该是枚举长度 */ -
注意18-20行枚举长度的方法。边界情况和下标计算不能弄错。同样的code在 Longest Palindromic Subsequence 也用到。
- 时间复杂度O(n^2), 空间复杂度O(n^2)
class Solution {
public:
bool firstWillWin(vector<int> &values) {
int n = values.size();
if ( n == 0)
return true;
int f[n][n];
f[0][0] = 0;
int j;
/* init */
for (int i = 1; i < n; i++) {
f[i][i] = values[i];
}
/* enumerate length */
for (int len = 2; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
j = i + len - 1;
f[i][j] = max(values[i] - f[i+1][j], values[j] - f[i][j-1]);
}
}
return f[0][n-1] >= 0;
}
};
Longest Palindromic Subsequence¶
- 区间型动态规划,子问题是去头去尾之后规模便小。写出状态后关键在于初始化,初始化的是对角线。
-
这道题的状态要相对好想,但是初始化和结果相对复杂。
* last step: a[i] == a[j] * state: f[i][j], LPS in string s[i], ... s[j] * equation: f[i][j] = max(f[i+1][j], f[i][j - 1], f[i-1][j-1]|s[i] == s[j]); * init: f[0][0] = 0, f[i][i] = 1; * if (s[i] == s[i + 1]) * f[i][i+1] = 2; * result: max(f[i][j])
public class Solution {
public int longestPalindromeSubseq(string s) {
int n = s.length();
if (n == 0)
return 0;
if (n == 1)
return 1;
int f[n][n];
int i, j, len;
f[0][0] = 0;
for (i = 1; i < n; i++) {
f[i][i] = 1;
}
for (i = 0; i < n - 1; i++) {
if (s[i] == s[i + 1]) {
f[i][i + 1] = 2;
} else {
f[i][i + 1] = 1;
}
}
/* enumerate the len */
for (len = 3; len <= n; len++) {
for (i = 0; i <= n - len; i++) {
j = i + len - 1;
/* init */
f[i][j] = f[i + 1][j]; // remove left
if (f[i][j - 1] > f[i][j]) { // remove right
f[i][j] = f[i][j - 1];
}
if (s[i] == s[j] && f[i + 1][j - 1] + 2 > f[i][j]) {
f[i][j] = f[i + 1][j - 1] + 2;
}
}
}
int res = 0;
for (i = 0; i < n; i++) {
for (j = i; j < n; j++) {
if (f[i][j] > res) {
res = f[i][j];
}
}
}
return res;
}
}
public class Solution {
int[][] f = null;
char[] s = null;
public void compute() {
if (f[i][j] != -1)
return;
if (i == j) {
f[i][j] = (s[i] == s[j]) ? 2 : 1;
return;
}
compute(i, j - 1);
compute(i + 1, j);
compute(i + 1, j - 1);
f[i][j] = Math.max(f[i][j - 1], f[i + 1][j]);
if (s[i] == s[j]) {
f[i][j] = Math.max(f[i][j], f[i + 1][j - 1] + 2);
}
}
public int longestPalindromeSubseq(String ss) {
s = ss.toCharArry();
int n = s.length;
if (n == 0) {
return 0;
}
f = new int[n][n];
for (int i = 0; i < n; ++i) {
for (int j = i; j < n; ++j) {
f[i][j] = -1;
}
}
compute(0, n 1);
return f[0][n - 1];
}
}
Note
划分型动态规划枚举的是长度而不是下标。
Burst Balloons¶
- This is a hard problem. you should very carefully to analyze the problem and write down the equation. Here is my first attempt, which made a mistake.
- You should play closely attention to the boundary of the for loop and the state transition equaltion.
- The time complexity is O(n^3) , and space complexity is O(n^3)
class Solution {
public:
/**
* @param nums a list of integer
* @return an integer, maximum coins
*/
int maxCoins(vector<int>& nums) {
int n = nums.size();
if (n == 1) {
return nums[0];
}
nums.insert(nums.begin(), 1);
nums.push_back(1);
int f[n + 2][n + 2];
int i, j, k, len;
/* f[i][j] = maxi<k<j{f[i][k] + f[k][j] + a[i] * a[k] * a[j]} */
for (i = 0; i < n + 1; i++) {
f[i][i + 1] = 0;
}
for (len = 3; len <= n + 2; len++) {/*边界:长度枚举到n+2 */
for (i = 0; i <= n - len + 2; i++) {/*边界:i是要从0开始,j到n+1, len = j - i + 1*/
j = i + len - 1;
f[i][j] = 0;
for (k = i + 1; k < j; k++) {/*边界: k是要burst的气球,我们说f[i][j]是不包括nums[i]和nums[j]的maxCoins*/
f[i][j] = max(f[i][j], f[i][k] + f[k][j] + nums[i] * nums[k] * nums[j]);
}
}
}
return f[0][n + 1];
}
};
Scramble String¶
- Here is the analysis
- 这里时间复杂度达到了O(n^4), 空间复杂度通过降维处理为O(n^3).
/* ---------------------
* | s1 | s2 | S
* ---------------------
* ---------------------
* | t1 | t2 | T
* ---------------------
* Last step: s1 <==> t1 && s2 <==> t2 OR s1 <==> t2 && S2 <==> t1
* Subproblem: s1 < S
* state: f[i][j][h][k] 代表是否S中从i到j的字符是由T中从h到k的字符scramble
* 因为长度一样,所以我们可以对状态进行降维处理。
* state: f[i][j][k]: 代表 s[i], ... s[i + k - 1] 是否是 t[j], ... t[j + k - * 1] scramble string.
* equation: f[i][j][k] = (f[i][j][w] && f[i + w][j + w] || f[i][j + k - w][w] && f[i + w][j][k - w]) for all 0 < w < k
* init: f[0][0][0] = ? (不重要)
* if (s[i] == t[j] && k == 1) {
* f[i][j][1] = true;
* }
*
*/
class Solution {
public:
/* *
* f[i][j][k] = OR_{0 < w < k}(f[i][j][w] && f[i+w][j+w][k-w]) OR (f[i][j+w][w] && f[i+w][j][)
*/
bool isScramble(string& s1, string& s2) {
int m = s1.length();
int n = s2.length();
if (m != n)
return false;
if (m == 0)
return true;
int f[n][n][n + 1];
int i, j, k, w;
/* init */
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
f[i][j][1] = s1[i] == s2[j];
}
}
for (k = 2; k <= n; k++) {
for (i = 0; i <= n - k; i++) {
for (j = 0; j <= n - k; j++) {
f[i][j][k] = false;
//enumerate partition position (s1's length)
for (w = 1; w < k; w++) {
// case 1: no swap match
if (f[i][j][w] && f[i + w][j + w][k - w]) {
f[i][j][k] = true;
break;
}
// case 2: swap match
if (f[i][j + k - w][w] && f[i + w][j][k - w]) {
f[i][j][k] = true;
break;
}
}
}
}
}
return f[0][0][n];
}
};
区间型动态规划总结¶
- 给定一个序列/字符串,进行一些操作
- 最后一步会将序列/字符串去头/去尾
- 剩下的会是一个区间
[i, j] - 状态自然定义为
f[i][j],表示面对子序列[i, …, j]时的最优性质 - 写程序时注意要枚举区间长度
Lecture 6¶
| Problem | Category |
|---|---|
| Longest Common Subsequence | |
| Interleaving String | |
| Edit Distance | |
| Distinct Subsequences | |
| Regular Expression Matching | |
| Wildcard Matching | |
| Ones and Zeroes |
Longest Common Subsequence¶
- State:
f[i][j], LCS of the firstichars from A and the firstjchars from B. - 定义状态是一定要注意下标的意义。在这里我们指的是前i个字符和前j个字符
- notice we can initialize the base case inside the loop.
class Solution {
public:
int longestCommonSubsequence(string A, string B) {
int m = A.length();
int n = B.length();
if (m == 0 || n == 0) {
return 0;
}
int f[m + 1][n + 1];
for (int i = 0; i <=m; ++i) {
for (int j = 0; j <=n; ++j) {
if (i == 0 || j == 0) {
f[i][j] = 0;
continue;
}
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (A[i - 1] == B[j - 1]) {
f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
}
}
return f[m][n];
}
};
Interleaving String¶
- Consider the where the last char in s3 came from, either from s1 or s2.
- state:
f[i][j], whether the firstifroms1and the firstjfroms2is interleaving of the firsti + jfroms3. - equation:
f[i][j] = (f[i][j - 1] && s[i + j - 1] == s2[j - 1]) || (f[i - 1][j] && s[i + j - 1] == s1[i - 1]) - we may attempt to have 3d matrix for the DP, but we can reduce the state representation by noticing the index of
s3can be derived from index ofs1ands2.
/* *
* last step: last s3[k - 1] == s1[m - 1] || s3[k - 1] == s2[n - 1]
* state: f[i][j][k]: s3[0],..s[k - 1] is interleaving of s1[0], ... s[i - 1] and s2[0], .. s[j - 1]
* equation 1: f[i][j][k] = (f[i][j - 1][k - 1] && s3[k - 1] == s1[i - 1])
* || (f[i - 1][j][k - 1] && s3[k - 1] == s2[j - 1])
* equation 2: f[i][j] = (f[i][j - 1] && s[i + j - 1] == s2[j - 1])
* || (f[i - 1][j] && s[i + j - 1] == s1[i - 1])
* init: f[0][0] = 1;
* f[0][0] = false if k > 0
*/
class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int m = s1.length();
int n = s2.length();
int k = s3.length();
if (m + n != k)
return false;
f[m + 1][n + 1];
for (int i = 0; i <= m; ++i) {
for (int j = 0; j <= n; ++j) {
if (i == 0 || j == 0) {
f[i][j] = false;
continue;
}
f[i][j] = false;
if (i > 0 && s1[i - 1] == s3[i + j - 1]) {
f[i][j] |= f[i - 1][j];
}
if (j > 0 && s2[j - 1] == s3[i + j - 1]) {
f[i][j] |= f[i][j - 1];
}
}
}
return f[m][n];
}
};
Edit Distance¶
- Notice the state update is not straightforward, you need to have the correct setting first and then write down the state transition equation. We define the state as follows
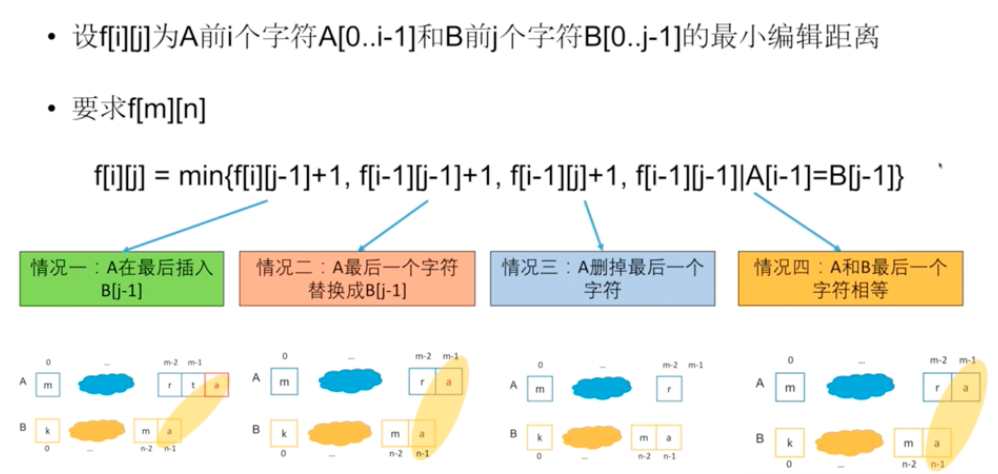
f[i][j]is the edit distance to make the firstichars inAand firstjchars inBthe same. - To make A and B the same, their last step need to be the same. There are three editing operations:
- Insert a char at the end of
A, so thatA[-1] == B[-1]. The state should be updated asf[i][j] = f[i][j - 1] + 1. This assignment operation purely mean that I can getf[i][j]from subproblem result. It doesn't indicate any of ther iteration of the string. You cannot have it likef[i][j] = f[i - 1][j - 1] + 1. - Delete a char at the end of
A, so thatA[-1] == B[-1]. The state update should bef[i][j] = f[i - 1][j] + 1. - Replace a char at the end of
A, so thatA[-1] == B[-1]. The state update should bef[i][j] = f[i - 1][j - 1] + 1. - No operation is needed, the last chars of the arrays are the same, such as
A[-1] == B[-1]. The state update should bef[i][j] = f[i - 1][j - 1].
- Insert a char at the end of
- notice the state represent the edit distance, don't try to correlate it to the index to the string after the edit, no string is changed while calculating the edit distance
f[i][j].
class Solution {
public:
/* *
* State: f[i][j] is the minimum number of steps to edit w1 to w2.
* f[i][j] = f[i][j - 1] + 1; insert
* = f[i - 1][j] + 1; delete
* = f[i - 1][j - 1] + 1; replace
* = f[i - 1][j - 1]; no opration needed
*/
int minDistance(string word1, string word2) {
int m = word1.length();
int n = word2.length();
int f[m + 1][n + 1];
f[0][0] = 0;
int i, j;
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
/* init */
if (i == 0) {
f[i][j] = j;
continue;
}
if (j == 0) {
f[i][j] = i;
continue;
}
// delete // insert
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
// replace
f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
// no operation
if (word1[i - 1] == word2[j - 1]) {
f[i][j] = min(f[i][j], f[i - 1][j - 1]);
}
}
}
return f[m][n];
};
};
class Solution {
public:
/* *
* State: f[i][j] is the minimum number of steps to convert w1 to w2. (len(w1) < len(w2))
* f[i][j] = f[i][j - 1] + 1; insert
* = f[i - 1][j] + 1; delete
* = f[i - 1][j - 1] + 1; replace
* = f[i - 1][j - 1]; no opration needed
*
*/
int minDistance(string word1, string word2) {
int m = word1.length();
int n = word2.length();
int f[m + 1][n + 1];
f[0][0] = 0;
int i, j;
int prev = -1;
int curr = 0;
for (i = 0; i <= m; i++) {
prev = curr;
curr = 1 - curr;
for (j = 0; j <= n; j++) {
/* init */
if (i == 0) {
f[curr][j] = j;
continue;
}
if (j == 0) {
f[curr][j] = i;
continue;
}
// delete // insert
f[curr][j] = min(f[prev][j] + 1, f[curr][j - 1] + 1);
// replace
f[curr][j] = min(f[curr][j], f[prev][j - 1] + 1);
// no operation
if (word1[i - 1] == word2[j - 1]) {
f[curr][j] = min(f[curr][j], f[prev][j - 1]);
}
}
}
return f[curr][n];
};
};
Note
- When using the
prevandcurrto index the 2d array, don't have to strictly follow the meaning of it. What you just need to make sure is the two row is rolling and not going to overwrite a useful value. - Notice the update of the "rolling index" is in between the two for loops. It has nothing to do with index
j.
Distinct Subsequence¶
- Last step,
t[n-1]match tos[m-1]or doesn't match. - State:
f[i][j]is the number of subsequence fort[0:j-2]ins[0:i-2] - state transition:
f[i][j] = f[i - 1][j - 1]|s[i - 1] == t[j - 1] + f[i - 1][j]
class Solution {
public:
/* *
* Last step: S[m - 1] in the
* S[0], ... S[m - 2], S[m - 1]
* T[0], ... T[n - 2], T[n - 1]
* State: f[i][j]: # of subsequence for the first j chars in T have in the first i chars in S
* Equation: f[i][j] = f[i - 1][j - 1]|S[i - 1] == T[j - 1] + f[i - 1][j]
* 1. S[m - 1] == T[n - 1]
* 1. f[i - 1][j - 1]
* 2. f[i - 1][j]
* 2. S[m - 1] != T[n - 1]
* 1. f[i - 1][j]
* Init: f[0][0] = 1;
* f[0][i] = 0;
* f[i][0] = 1;
*/
int numDistinct(string &S, string &T) {
int m = S.length();
int n = T.length();
int f[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 && j == 0) {
f[i][j] = 1;
continue;
}
if (i == 0) {
f[i][j] = 0;
continue;
}
if (j == 0) {
f[i][j] = 1;
continue;
}
f[i][j] = f[i - 1][j];
if (S[i - 1] == T[j - 1]) {
f[i][j] += f[i - 1][j - 1];
}
}
}
return f[m][n];
}
};
Regular Expression Matching¶
class Solution {
public:
/* *
* Last step (last char to match in the strings):
* p[j - 1] != s[i - 1] ==> f[i][j] = false;
* p[j - 1] == s[i - 1] ==> f[i][j] = f[i - 1][j - 1];
* p[j - 1] == '.' ==> f[i][j] = f[i - 1][j - 1]
*
* p[j - 1] == '*',
* case 1 p[j - 2] == '.' ==> f[i][j] = f[i - 1][j]; ??? why not f[i][j] = true;
* p[j - 2] != '.'
* p[j - 2] == s[i - 1] ==> f[i][j] = f[i'][j - 2] | i' is the length not equal to p[j - 2].
* which one? /
* \
* case 2 p[j - 2] == s[i - 1] ==> f[i][j] = f[i - 1][j]
* p[j - 2] != s[i - 1] ==> f[i][j] = f[i][j - 2];
*
* We see that case 1 and case 2 could be combined and put inside one if statement.
* State: f[i][j]: the first i chars form s match regex the first j chars from p
* Equation: f[i][j] =
* Init: f[0][0] = 0;
* f[0][j] = ture; if p[j - 1] == '*'
* f[i][0] = false;
*/
bool isMatch(const char *s, const char *p) {
int i, j;
int m = 0;
int n = 0;
while (s[m] != '\0') {
m++;
}
while (p[n] != '\0') {
n++;
}
int f[m + 1][n + 1];
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 && j == 0) {
f[i][j] = true;
continue;
}
if (j == 0) {
f[i][j] = false;
continue;
}
f[i][j] = false;
if (p[j - 1] == '*') {
// matched one char at end of s, s=[----]a, p=[-----]a*
if (i > 0 && j > 1 && (p[j - 2] == '.' || p[j - 2] == s[i - 1])) {
f[i][j] |= f[i - 1][j]; //use whole p to match s[0, ... i - 2]
}
// don't care the a* or .*,
// match previous chars s=[-----a], p=[------]a*
if (j > 1) {
f[i][j] |= f[i][j - 2];
}
} else if (i > 0 && (p[j - 1] == '.' || p[j - 1] == s[i - 1])) {
f[i][j] = f[i - 1][j - 1];
}
}
}
return f[m][n];
}
};
// The idea is to deal with each case one by one.
class Solution {
public:
bool isMatch(string s, string p) {
/* base cases when none left or only one char left */
if (p.empty()) return s.empty();
if (p.length() == 1) {
return (s.length() == 1 && (s[0] == p[0] || p[0] == '.'));
}
if (p[1] != '*') {
if (s.empty()) return false;
return (s[0] == p[0] || p[0] == '.') && isMatch(s.substr(1), p.substr(1));
}
/* p[1] == '*' */
while (!s.empty() && (s[0] == p[0] || p[0] == '.')) {
/* consider the case: s="aaaabcd", p=".*b*cd"*/
if (isMatch(s, p.substr(2))) return true;
s = s.substr(1);
}
/* consider the case: s="aaaaa", p="a*" and case s="aaaaa", p="a*b" */
return isMatch(s, p.substr(2)); /* how comes? */
}
};
Wildcard Matching¶
- 不需要知道''最多能匹配几个字符。在当前step只需考虑用''去匹配一个字符或者完全不匹配就覆盖了 所有的情况。至于最终可以匹配几个,是在多个step中的信息。当前step并不需要关心.
- When
p[j - 1] == '*', since we don't know '' match how many chars in s? In the first solution, I used a third loop to check. We can think it in this way, forp[j - 1] == '*', we can use '' to match the trailing character or not to use '*' to match previously. the we havef[i][j] = f[i - 1][j] | f[i][j - 1].
class Solution {
public:
/* *
* last step:
* p[j - 1] == '?'
* f[i][j] = f[i - 1][j - 1]
* s[i - 1] == p[j - 1]
* f[i][j] = f[i - 1][j - 1]
* p[j - 1] == '*', ('*' may match k of trailng characters from s, but we don't know how many)
* f[i][j] = f[i][j - 1] OR f[i - 1][j - 1] OR f[i - 2][j - 1], .. f[i - k][j - 1]
* State: f[i][j]: the first i chars from s match the first j letters from p
* Equation:
* Init: f[0][0] = true;
* f[i][0] = false;
* f[0][j] = true; if (p[j - 1] == "*" && j == 1)
* calculate by DP:
* f[0][j] = false; if (j > 1)
*/
bool isMatch(const char *s, const char *p) {
int m = 0;
int n = 0;
int i, j, k;
while (s[m] != '\0') {
m++;
}
while (p[n] != '\0') {
n++;
}
int f[m + 1][n + 1];
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 && j == 0) {
f[i][j] = true;
continue;
}
if (j == 0) {
f[i][j] = false;
continue;
}
f[i][j] = false;
if (p[j - 1] == '*') {
// k == i indicate the special case: f[0][1] (s="", p="*")
for (k = 0; k <= i; k++) {
f[i][j] |= f[i - k][j - 1];
}
} else {
if (i > 0 && (p[j - 1] == '?' || s[i - 1] == p[j - 1])) {
f[i][j] = f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
};
class Solution {
public:
bool isMatch(const char *s, const char *p) {
// write your code here
int m = 0;
int n = 0;
int i, j, k;
while (s[m] != '\0') {
m++;
}
while (p[n] != '\0') {
n++;
}
int f[m + 1][n + 1];
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 && j == 0) {
f[i][j] = true;
continue;
}
if (j == 0) {
f[i][j] = false;
continue;
}
f[i][j] = false;
if (p[j - 1] == '*') {
f[i][j] = f[i][j - 1]; // ignore the '*', match nothing
if (i > 0) {
f[i][j] |= f[i - 1][j]; // match the trailing char from s and continue
}
} else {
if (i > 0 && (p[j - 1] == '?' || s[i - 1] == p[j - 1])) {
f[i][j] = f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
};
Ones and Zeroes¶
- This is essentially a backpack problem see the backpack problem. The key to solve the problem is taking the last item or do not take the last item.
- 技巧:背包问题的“最后一步”是指最后一个“物品”在结果中或者不再结果中.
class Solution {
public:
/* *
* 背包问题,最后一个进“背包”,最后一个不进。
* State: f[i][j][k]: maximum of k strs can be formed by i zeros and j ones.
* Equation: f[i][j][k] = max(f[i][j][k - 1], f[i - a][j - b][k - 1] + 1| i > a and j > b)
* Init: f[i][j][0] = 0
*
*/
int findMaxForm(vector<string>& strs, int m, int n) {
int len = strs.size();
int cnt0[len];
int cnt1[len];
int i, j, k;
int f[m + 1][n + 1][len + 1];
/* count all the zeros and ones */
for (k = 0; k < len; k++) {
cnt0[k] = 0;
cnt1[k] = 0;
for (i = 0; i < strs[k].length(); i++) {
if (strs[k][i] == '0') {
cnt0[k]++;
} else {
cnt1[k]++;
}
}
}
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
f[i][j][0] = 0;
}
}
/* k started from 1 */
for (k = 1; k <= len; k++) {
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
f[i][j][k] = f[i][j][k - 1];
if (i >= cnt0[k - 1] && j >= cnt1[k - 1]) {
f[i][j][k] = max(f[i][j][k], f[i - cnt0[k - 1]][j - cnt1[k - 1]][k - 1] + 1);
}
}
}
}
return f[m][n][len];
}
};
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int len = strs.size();
int cnt0[len];
int cnt1[len];
int i, j, k;
/* count all the zeros and ones */
for (k = 0; k < len; k++) {
cnt0[k] = 0;
cnt1[k] = 0;
for (i = 0; i < strs[k].length(); i++) {
if (strs[k][i] == '0') {
cnt0[k]++;
} else {
cnt1[k]++;
}
}
}
int f[m + 1][n + 1][len + 1];
int prev, curr = 0;
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
f[i][j][curr] = 0;
}
}
/* k started from 1 */
for (k = 1; k <= len; k++) {
prev = curr;
curr = 1 - curr;
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
f[i][j][curr] = f[i][j][prev];
if (i >= cnt0[k - 1] && j >= cnt1[k - 1]) {
f[i][j][curr] = max(f[i][j][curr], f[i - cnt0[k - 1]][j - cnt1[k - 1]][prev] + 1);
}
}
}
}
return f[m][n][curr];
}
};
双序列型动态规划总结¶
- 两个一维序列/字符串
- 突破口
- 串A和串B的最后一个字符是否匹配
- 是否需要串A/串B的最后一个字符
- 缩减问题规模
- 数组下标表示序列
A前i个,序列B前j个:f[i][j] - 初始条件和边界情况
- 空串如何处理
- 计数型(情况1+情况2+…)以及最值型(min/max{情况1,情况2,…})
- 匹配的情况下勿忘+1(操作数多1次,匹配长度多1)
Lecture 7¶
| Problem | Category |
|---|---|
| Minimum Adjustment Cost | |
| K Sum | 背包型 |
| Longest Increasing Subsequence | 序列型 |
| K Edit Distance | 双序列 + Trie |
| Frog Jump | 坐标 + 状态 |
| Maximal Square | 坐标 |
| Maximal Rectangle |
Minimum Adjustment Cost¶
- The key is how to come up the last step and the induction. The key is to come up a sensable modle of the problem. See the analysis in the code comments.
- The hard part of the problem is how to prove the the range:
1 <= B[i] <= 100, so that we can create the state arrayf[n + 1][100 + 1] - The initial value of this DP problem is not obvious. You have to pay attention to the initial condition of this problem, it different from the provious DP problems.
class Solution {
public:
/**
* 技巧:要看作把A数组通过变化变成B数组。最后一步考虑把A[i]变成B[i].
* 这样比在A的基础上变化更容易考虑递推关系
* Last step: change A[i] to B[i], result[i] = result[i - 1] + abs(B[i] - A[i])
* State: f[i][j]: the cost of changing the first i element in A,
* and the last elemnet A[i - 1] changed is changed to j (j == B[i])
* Induction: A[i - 1] --> j, A[i - 2] --> k, |j - k| < target ==> j - target <= k <= j + target
* Equation: f[i][j] = min_{j - target <= k <= j + target, 1 <= k <= 100}(f[i - 1][k] + abs(j - A[i]))
* Init: f[0][0] = ?
* f[1][k] = abs(k - A[0])
*/
int MinAdjustmentCost(vector<int> A, int target) {
int n = A.size();
int f[n + 1][100 + 1];
int i, j, k;
for (j = 1; j <= 100; j++) {
f[1][j] = abs(j - A[0]);
}
for (i = 2; i <= n; i++) {
for (j = 1; j <= 100; j++) {
f[i][j] = INT_MAX;
for (k = j - target; k <= j + target; k++) {
if (k < 1 || k > 100) {
continue;
}
f[i][j] = min(f[i][j], f[i - 1][k] + abs(j - A[i - 1]));
}
}
}
int res = INT_MAX;
for (j = 1; j <= 100; j++) {
res = min(res, f[n][j]);
}
return res;
}
};
Note
The space complexity is O(100n). The time complexity is O(1002n).
K Sum¶
- This is a backpack problem which is very similar to the problem Backpack VI
- 背包问题的话,总承重要进状态,也就是说
target要进状态。其他还有什么要进状态呢?这就要求认真分析题目。 - 对于这种类似求不放回的组合数的过程,不要尝试去用循环来决定某一个元素是否被选中。而是要结合 induction的想法,从某个特殊的步骤着眼,在这个步骤中考虑选中或者不选某个元素(本身带有循环的意思, 任何一个元素只能被选中一次,和不选一次)
- 下面代码注释中给出了我最初的错误分析,随后又给出了正确的分析。对比二者不同,争取以后少犯类似错误。
- 关键需要注意的是初始化。先把
f[0][q][s]全部初始化为0,然后再初始化f[0][0][0]。这两个步骤不能颠倒顺序, - 注意也可以在for loop中初始化f[0][0][0]。
- Time complexity O(n \cdot k \cdot \text{target}), space complexity O(n \cdot k \cdot \text{target}). We can use rolling array to reduce the space complexity to O(k \cdot \text{target}).
class Solution {
public:
/**
* This is a backpack problem,
* Last step: A[i] is selected or not selected.
* State: f[i][j]: total solution of i element can sum up to j.
* Equation: f[i][j] = f[i - 1][j] + f[i - 1][j - A[i - 1]]|j > A[i - 1] for all i == k.
* Equation: f[i][j] = sum(f[i - 1][j - A[k]] | 0 <= k <= i - 1, j > A[k]).
* Init: f[0][0] = 1; // ?
* f[0][j] = 0
* ******************** WRONG *********************************
* ******************** CORRECT *******************************
* Last step: A[i - 1] is selected or not selected.
* If selected, we should select k - 1 numbers from A[0], .. A[n - 2] that sum to target - A[i - 1].
* If not selected, we should select k number from A[0], .. A[n - 2] that sum to target.
* State: f[i][k][s]: total solution of selecting k element from first i element that sum up to j.
* Equation: f[i][k][s] = f[i - 1][k][s] + f[i - 1][k - 1][s - A[i - 1]]|s > A[i - 1].
* Init: f[0][0][0] = 1; // ?
* f[0][k][s] = 0
*
*/
int kSum(vector<int> A, int k, int target) {
// wirte your code here
int n = A.size();
int f[n + 1][k + 1][target + 1];
int i, q, s;
// init
for (q = 0; q <= k; q++) {
for (s = 0; s <= target; s++) {
f[0][q][s] = 0;
}
}
f[0][0][0] = 1;
for (i = 1; i <= n; i++) {
for (q = 0; q <= k; q++) {
for (s = 0; s <= target; s++) {
// not select A[i - 1]
f[i][q][s] = f[i - 1][q][s];
// select A[i - 1]
if (q >= 1 && s >= A[i - 1]) {
f[i][q][s] += f[i - 1][q - 1][s - A[i - 1]];
}
}
}
}
return f[n][k][target];
}
};
class Solution {
public:
int kSum(vector<int> A, int k, int target) {
// wirte your code here
int n = A.size();
int f[n + 1][k + 1][target + 1];
int i, q, s;
int curr = 0, prev = 0;
// init
for (q = 0; q <= k; q++) {
for (s = 0; s <= target; s++) {
f[curr][q][s] = 0;
}
}
f[curr][0][0] = 1;
for (i = 1; i <= n; i++) {
prev = curr;
curr = 1 - curr ;
for (q = 0; q <= k; q++) {
for (s = 0; s <= target; s++) {
// not select A[i - 1]
f[curr][q][s] = f[prev][q][s];
// select A[i - 1]
if (q >= 1 && s >= A[i - 1]) {
f[curr][q][s] += f[prev][q - 1][s - A[i - 1]];
}
}
}
}
return f[curr][k][target];
}
};
Longest Increasing Subsequence¶
K Edit Distance¶
Frog Jump¶
- You could use naive solution to iterate all the possible cases and use memoization to speed up.
- In that case, you can also use binary search to located a stone in the array which help to improve the complexity.
- But the best solution is to use a map to keep all the possible steps for a stone.
class Solution {
public:
bool canCross(vector<int>& stones) {
int n = stones.size();
unordered_map<int, unordered_set<int>> hmap;
for (int i = 0; i < stones.size(); i++) {
hmap[stones[i]] = unordered_set<int>();
}
hmap[stones[0]].insert(0);
for (int i = 0; i < stones.size(); i++) {
for (int k: hmap[stones[i]]) {
for (int s = k - 1; s <= k + 1; s++) {
if (s > 0 && hmap.find(stones[i] + s) != hmap.end()) {
hmap[stones[i] + s].insert(s);
}
}
}
}
return hmap[stones[n - 1]].size() > 0;
}
};