Graph¶

Representations¶

Edge lists¶

An edge is represented using an array of two vertex numbers or objects contain the vertex numbers. Weights can be added as the third number or another member of the objects.

Example: [[0,1], [0,6], [0,8], [1,4], [1,6], [1,9], [2,4], [2,6], [3,4], [3,5]]
Space: $\Theta(E)$
Search edge: $O(E)$

Adjacency matrix¶

Use a matrix[i][j] to represent the edges. 1 is connected, 0 is not connected.

Example:

[ [0, 1, 0, 0, 0, 0, 1, 0, 1, 0],
[1, 0, 0, 0, 1, 0, 1, 0, 0, 1],
[0, 0, 0, 0, 1, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 0, 0, 1, 0],
[0, 1, 1, 1, 0, 1, 0, 0, 0, 1],
[0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 0],
[0, 1, 0, 0, 1, 0, 0, 1, 0, 0] ]

Check edge (i, j) exists: $O(1)$
Space: $\Theta(V^2)$
Search djacent vertex: $O(V)$
For undirected graph, adjacency matrix is symmetric. For a directed graph, the adjacency matrix need not be symmetric.

Adjacency list¶

Representing a graph with adjacency lists combines adjacency matrices with edge lists. For each vertex i, store an array of the vertices adjacent to it. Each vertex has a list.

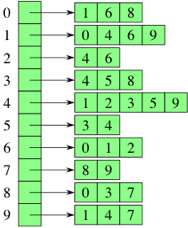
Adjacency list

Space: $\Theta(2E)$ for undirected graph. $\Theta(E)$ for directed graph.
Check edge (i, j) exists: $O(d)$ , d is the degree of the vertex i. $0 \leq d \leq V - 1$ .
If the graph is weighted, then each item in each adjacency list is either a two-item array or an object, giving the vertex number and the edge weight.

Representing graphs

Algorithms¶

Weighted Graph
Unweighted Graph
Directed Graph
Undirected Graph
Graph Traversal
Single Source Shortest Path
Connected components
Minimum spanning tree

Kosaraju's Two-pass algorithm¶

Reverse each arc of the original graph.
First run of the DFS-Loop to computer the "finish" time of each node in the reversed graph. Book keeping:
- The "source node of a node". A source node is the first node in the DFS tree.
- The "finish time of a node".
Second run of the DFS-Loop to computer the strongly connected components (SCC). The SCC is represented by the source node.

Dijkstra algorithm (No negative edge)¶

Dijkstra algorithm implementation need one data structure (think of it as an array) to record the path distance, another data structure (priority queue) to maintain the min-heap which is ordered by the key of the edge weights. The algorithm greedily select the smallest edge from the queue and update the optimal solution so far (called relaxation in graph algorithm jargon).
Dijkstra algorithm Implemention requires to maintain two invariant, 1. All the vertices $w_i$ that not in $S$ will be kept in the heap. 2. The key should be the minimum weight of all the edges who's tail in $S$ , head point to $w_i$ . In every iteration, each $w_i$ need to run a local turnament to decide its new key and then update the heap.
To compare Dijkastra to BFS, when you visit a new node, Dijkastra will do a relaxation (update keys by local turnament and reinsert heap) while BFS simply add the node to the queue.

Dijkstra Algorith

Dijkastra algorithm psudo code

INITIALIZE-SINGLE-SOURCE(G, s)
  for each vertex v in G.V:
    v.d = inf
    v.parent = null
  s.d = 0

RELAX(u, v, w)
  if v.d > u.d + w(u, v)
    v.d = u.d + w(u, v)
    v.parent = u

DIJKSTRA(G,w,s)
  INITIALIZE-SINGLE-SOURCE(G, s)
  S = None
  Q = G.V
  while Q != None
    u = EXTRACT-MIN(Q)
    S = S + {u}
    for each vertex v in G.adj[u]:
      RELAX(u, v, w)

Bellman-Ford¶

Bellman-Ford algorithm take care of negative edges in finding the single source shortest path in a graph. In addition, it also can be used to detect negative cycles reachable from the source. Notice Bellman-Ford algorithm can be optimized by exit when there is no new update happening. However, the worst case runtime is still $O(V \cdot, E)$ .

Bellman-Ford algorithm psudo code

function BellmanFord(list vertices, list edges, vertex source) is

    // This implementation takes in a graph, represented as
    // lists of vertices (represented as integers [0..n-1]) and edges,
    // and fills two arrays (distance and predecessor) holding
    // the shortest path from the source to each vertex

    distance := list of size n
    predecessor := list of size n

    // Step 1: initialize graph
    for each vertex v in vertices do
        distance[v] := inf             // Initialize the distance to all vertices to infinity
        predecessor[v] := null         // And having a null predecessor

    distance[source] := 0              // The distance from the source to itself is, of course, zero

    // Step 2: relax edges repeatedly
    repeat |V|−1 times:
        for each edge (u, v) with weight w in edges do
            if distance[u] + w < distance[v] then
                distance[v] := distance[u] + w
                predecessor[v] := u

    // Step 3: check for negative-weight cycles
    for each edge (u, v) with weight w in edges do
        if distance[u] + w < distance[v] then
            error "Graph contains a negative-weight cycle"

    return distance, predecessor

Shortest Path Faster Algorithm¶

The algorithm is an improvement on Bellman-Ford algorithm. The idea is to limit the relaxation operation on only those nodes that have been relaxed before. We can use a queue to keep such nodes. However, the worst case runtime complexity is the same as Bellman-Ford, it is still $O(V \cdot, E)$ .

procedure Shortest-Path-Faster-Algorithm(G, s)
  1    for each vertex v ≠ s in V(G)
  2        d(v) := ∞
  3    d(s) := 0
  4    push s into Q
  5    while Q is not empty do
  6        u := poll Q
  7        for each edge (u, v) in E(G) do
  8            if d(u) + w(u, v) < d(v) then
  9                d(v) := d(u) + w(u, v)
 10                if v is not in Q then
 11                    push v into Q

Bipartise¶

One algorithm to use in graph bipartition is using coloring, namely apply DFS and color each node with different colors when visited them differently.

Directed graph strongly connected components¶

Interivew Strategy¶

Clarification questions¶

What's the input scale? What's the limit of depth?
Does the graph have self-edge or duplications? what's the corresponding return value should be if yes?

Solving graph problems¶

DFS/BFS/UF -> topological -> Bellman Ford -> Dijkastra ->
To traverse a cyclic graph, we could not use visited, think of remove a edge after visited it. One example problem is 332. Reconstruct Itinerary

Problems¶

332. Reconstruct Itinerary¶

407. Trapping Rain Water II¶

class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        if (heightMap.empty()) return 0;
        int m = heightMap.size();
        int n = m ? heightMap[0].size() : 0;
        if (m <= 2 || n <= 2) {
            return 0;
        }

        int res = 0, mx = 0;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        vector<vector<bool>> visited(m, vector<bool>(n, false));

        int x[4] = {-1, 0, 1, 0};
        int y[4] = {0, 1, 0, -1};

        // initialize the pq.
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    pq.push({heightMap[i][j], i * n + j});
                    visited[i][j] = true;
                }
            }
        }

        while (!pq.empty()) {
            auto t = pq.top(); pq.pop();
            int h = t.first;
            int i = t.second / n;
            int j = t.second % n;
            mx = max(h, mx);
            for (int k = 0; k < 4; k++) {
                int p = i + x[k];
                int q = j + y[k];
                if (p >= 0 && p < m && q >= 0 && q < n && !visited[p][q]) {
                    visited[p][q] = true;
                    if (heightMap[p][q] < mx) {
                        res += mx - heightMap[p][q];
                    }

                    pq.push({heightMap[p][q], p * n + q});
                }
            }
        }

        return res;
    }
};

Critical Connections in a Network¶

Critical Routers ¶

743. Network Delay Time¶

Solution 1 Dijkstra algorithm
What's the key for heap node?
What's the data structure is needed? (dist array, and a heap)
Solution 2 Bellman Ford algorithm
Solution 3 Shortest Path Best algorithm

=== C++ Dijkstra

```c++
class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        vector<vector<pair<int, int>>> graph(n + 1, vector<pair<int, int>>());
        for (auto& t: times) {
            graph[t[0]].push_back({t[1], t[2]});
        }

        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        pq.push({0, k});
        vector<int> dist(n + 1, INT_MAX);
        dist[k] = 0;

        while (!pq.empty()) {
            pair<int, int> t = pq.top();
            pq.pop();

            int u = t.second;
            for (auto x: graph[u]) {
                int v = x.first;
                int w = x.second;

                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    pq.push({dist[v], v});
                }
            }
        }

        int res = *max_element(dist.begin() + 1, dist.end());

        return res == INT_MAX ? -1 : res;
    }
};
```

=== C++ Bellman Ford

```c++
class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        vector<int> dist(n + 1, INT_MAX);
        dist[k] = 0;
        for (int i = 0; i < n; ++i) {
            for (auto& t : times) {
                int u = t[0], v = t[1], w = t[2];
                if (dist[u] != INT_MAX && dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                }
            }
        }

        int res = *max_element(dist.begin() + 1, dist.end());

        return res == INT_MAX ? -1 : res;
    }
};
```

778. Swim in Rising Water¶

Solution 1 Binary search + DFS Solution 2 Dijkstra

C++ Binary Search + DFS

class Solution {
    int x[4] = {0, -1, 0, 1};
    int y[4] = {-1, 0, 1, 0};
public:
    int swimInWater(vector<vector<int>>& grid) {
        int n = grid.size();
        int begin = grid[0][0], end = n * n - 1;
        // binary search find a path with mini elevation
        while (begin < end) {
            int mid = begin + (end - begin) / 2;
            if (pathExist(grid, mid)) {
                end = mid;
            } else {
                begin = mid + 1;
            }
        }

        return begin;
    }

    bool pathExist(vector<vector<int>> & grid, int mid) {
        int n = grid.size();
        vector<vector<int>> visited(n, vector<int>(n, 0));
        return dfs_helper(grid, visited, n, mid, 0, 0);
    }

    bool dfs_helper(vector<vector<int>> & grid, vector<vector<int>>& visited,
                    int n, int mid, int i, int j) {
        visited[i][j] = 1;
        for (int k = 0; k < 4; ++k) {
            int a = i + x[k];
            int b = j + y[k];
            if (a < 0 || a >= n || b < 0 || b >= n || visited[a][b] == 1 || grid[a][b] > mid) continue;
            if (a == n - 1 && b == n - 1) return true;
            if (dfs_helper(grid, visited, n, mid, a, b)) return true;
        }

        return false;
    }
};

C++ Dijkstra

class Solution {
    int d[5] = {0, -1, 0, 1, 0};
public:
    int swimInWater(vector<vector<int>>& grid) {
        int n = grid.size();

        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        pq.push({grid[0][0], 0});
        vector<vector<int>> visited(n, vector<int>(n, 0));
        visited[0][0] = 1;

        int res = 0;

        while (!pq.empty()) {
            pair<int, int> t = pq.top();
            pq.pop();
            int x = t.second / n;
            int y = t.second % n;

            res = max(res, t.first);

            if (x == n - 1 && y == n - 1)
                break;

            for (int i = 0; i < 4; ++i) {
                int a = x + d[i];
                int b = y + d[i + 1];

                if (a >= 0 && a < n && b >= 0 && b < n && visited[a][b] == 0) {
                    visited[a][b] = 1;
                    pq.push({grid[a][b], a * n + b});
                }
            }
        }

        return res;
    }
};

785. Is Graph Bipartite?¶

Solution 1 Coloring neighboring nodes with alternative color

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        vector<int> visited(n, -1);

        for (int i = 0; i < n; ++i) {
            if (visited[i] == -1 && !dfs_helper(graph, visited, i, 1)) {
                return false;
            }
        }

        return true;
    }

    bool dfs_helper(vector<vector<int>>& graph, vector<int>& visited, int i, int color) {
        if (visited[i] != -1) {
            return visited[i] == color; // the color is ok
        }

        visited[i] = color; // not colored before, now color it
        for (auto v : graph[i]) {
            if (!dfs_helper(graph, visited, v, 1 - color)) {
                return false;
            }
        }

        return true;
    }
};

1102. Path With Maximum Minimum Value¶

Solution 1 Dijkstra Solution 2 Union-Find

Python Union Find

class Solution:
    def maximumMinimumPath(self, A: List[List[int]]) -> int:
        R, C = len(A), len(A[0])
        parent = [i for i in range(R * C)]
        dire = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        seen = [[0 for _ in range(C)] for _ in range(R)]

        def find(x):
            if parent[x] != x:
                parent[x] = find(parent[x])
            return parent[x]

        def union(x, y):
            rx, ry = find(x), find(y)
            if rx != ry:
                parent[ry] = rx

        points = [(x, y) for x in range(R) for y in range(C)]
        points.sort(key = lambda x: A[x[0]][x[1]], reverse = True)

        for x, y in points:
            seen[x][y] = 1
            for dx, dy in dire:
                nx, ny = x + dx, y + dy
                if 0 <= nx < R and 0 <= ny < C and seen[nx][ny]:
                    union(x * C + y, nx * C + ny)
            if find(0) == find(R * C - 1):
                return A[x][y]
        return -1

C++ Dijkstra

class Solution {
public:
    int maximumMinimumPath(vector<vector<int>>& A) {
        int m = A.size();
        int n = A[0].size();

        int res = INT_MAX;
        priority_queue<pair<int, int>, vector<pair<int, int>>> pq; // max heap.
        pq.emplace(A[0][0], 0);
        vector<vector<int>> visited(m, vector<int>(n, 0));
        visited[0][0] = -1;

        int d[5] = {0, 1, 0, -1, 0};

        while (!pq.empty()) {
            pair<int, int> t = pq.top(); pq.pop();
            int cost = t.first;
            int x = t.second / n;
            int y = t.second % n;

            res = min(res, cost);

            if (x == m - 1 && y == n - 1)
                break;

            for (int k = 0; k < 4; k++) {
                int r = x + d[k];
                int c = y + d[k + 1];

                if (r < 0 || r >= m || c < 0 || c >= n || visited[r][c] < 0) continue;

                pq.emplace(A[r][c], r * n + c);
                visited[r][c] = -1;
            }
        }

        return res;
    }
};

1514. Path with Maximum Probability¶

class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges,
        vector<double>& succProb, int start, int end) {

        unordered_map<int, vector<pair<int, double>>> graph;

        for (int i = 0; i < edges.size(); ++i) {
            graph[edges[i][0]].push_back({edges[i][1], succProb[i]});
            graph[edges[i][1]].push_back({edges[i][0], succProb[i]});
        }

        vector<double> prob(n, 0.0);
        prob[start] = 1.0;

        priority_queue<pair<double, int>> pq;
        pq.push({1.0, start});

        while (!pq.empty()) {
            pair<double, int> u = pq.top(); pq.pop();

            for (auto vp: graph[u.second]) {
                int v = vp.first;
                double p = vp.second;
                if (prob[v] < p * prob[u.second]) {
                    prob[v] = p * prob[u.second];
                    pq.push({prob[v], v});
                }
            }
        }

        return prob[end];
    }
};

1631. Path With Minimum Effort ¶

C++ Dijkstra

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size();
        int n = heights[0].size();

        vector<vector<int>> dist(m, vector<int>(n, INT_MAX)); // min distance found so far.
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;

        int d[5] = {0, 1, 0, -1, 0};

        pq.emplace(0, 0); // first: min effort, second: encoded (x, y) (=x * n + y);

        while (!pq.empty()) {
            pair<int, int> t = pq.top();
            int effort = t.first;
            int x = t.second / n;
            int y = t.second % n;
            pq.pop();

            if (x == m - 1 && y == n - 1)
                return effort;

            for (int k = 0; k < 4; ++k) {
                int a = x + d[k];
                int b = y + d[k + 1];

                if (a < 0 || a >= m || b < 0 || b >= n) continue;
                int currEffort = max(effort, abs(heights[a][b] - heights[x][y]));

                if (currEffort < dist[a][b]) {
                    dist[a][b] = currEffort;
                    pq.push({currEffort, a * n + b});
                }
            }

        }

        return -1;
    }
};

Python Dijkstra

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        m, n = map(len, [heights, heights[0]])
        efforts = [[math.inf] * n for _ in range(m)]
        efforts[0][0] = 0
        heap = [(0, 0, 0)]

        while heap:
            effort, x, y = heapq.heappop(heap);

            if x == m - 1 and y == n - 1:
                return effort

            for i, j in (x, y - 1), (x, y + 1), (x - 1, y), (x + 1, y):
                if i < 0 or i >= m or j < 0 or j >= n:
                    continue
                currEffort = max(effort, abs(heights[x][y] - heights[i][j]))
                if efforts[i][j] > currEffort:
                    efforts[i][j] = currEffort
                    heapq.heappush(heap, (currEffort, i, j))

Java Dijkstra

class Solution {
    private int[] d = {0, 1, 0, -1, 0};

    public int minimumEffortPath(int[][] heights) {
        int lo = 0, hi = 1_000_000;
        while (lo < hi) {
            int effort = lo + (hi - lo) / 2;
            if (isPath(heights, effort)) {
                hi = effort;
            }else {
                lo = effort + 1;
            }
        }
        return lo;
    }

    private boolean isPath(int[][] h, int effort) {
        int m = h.length, n = h[0].length;
        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[2]);
        Set<Integer> seen = new HashSet<>();
        seen.add(0);
        while (!q.isEmpty()) {
            int[] cur = q.poll();
            int x = cur[0], y = cur[1];
            if (x == m - 1 && y == n - 1) {
                return true;
            }
            for (int k = 0; k < 4; ++k) {
                int r = x + d[k], c = y + d[k + 1];
                if (0 <= r && r < m && 0 <= c && c < n &&
                    effort >= Math.abs(h[r][c] - h[x][y]) && seen.add(r * n + c)) {
                    q.offer(new int[]{r, c});
                }
            }
        }

        return false;
    }
}

Java Binary search + BFS

class Solution {
    private int[] d = {0, 1, 0, -1, 0};
    public int minimumEffortPath(int[][] heights) {
        int lo = 0, hi = 1_000_000;
        while (lo < hi) {
            int mid = lo + (hi - lo) / 2;
            if (isPath(heights, mid)) {
                hi = mid;
            } else {
                lo = mid + 1;
            }
        }

        return lo;
    }

    private boolean isPath(int[][] h, int mid) {
        int m = h.length, n = h[0].length;
        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[2]);
        Set<Integer> seen = new HashSet<>();
        seen.add(0);

        while (!q.isEmpty()) {
            int[] cur = q.poll();
            int x = cur[0], y = cur[1];
            if (x == m - 1 && y == n - 1)
                return true;

            for (int k = 0; k < 4; k++) {
                int r = x + d[k], c = y + d[k + 1];
                if (0 <= r && r < m && 0 <= c && c < n &&
                    mid >= Math.abs(h[r][c] - h[x][y]) && seen.add(r * n + c)) {
                    q.offer(new int[]{r, c});
                }
            }
        }

        return false;
    }
}

Graph¶

Representations¶

Edge lists¶

Adjacency matrix¶

Adjacency list¶

Algorithms¶

Kosaraju's Two-pass algorithm¶

Dijkstra algorithm (No negative edge)¶

Bellman-Ford¶

Shortest Path Faster Algorithm¶

Bipartise¶

Directed graph strongly connected components¶

Interivew Strategy¶

Clarification questions¶

Solving graph problems¶

Problems¶

332. Reconstruct Itinerary¶

407. Trapping Rain Water II¶

Critical Connections in a Network¶

Critical Routers¶

743. Network Delay Time¶

778. Swim in Rising Water¶

785. Is Graph Bipartite?¶

1102. Path With Maximum Minimum Value¶

1514. Path with Maximum Probability¶

1631. Path With Minimum Effort¶

Critical Routers ¶

1631. Path With Minimum Effort ¶