Union Find¶
Introduction¶
Union Find problem can be used to model the dynamic connectivity problem. Briefly, given a set of N objects, implement a union command to connect two objects, and a find (or connected) command to query whether exist a path connecting the two objects.
To model the connections, we assume the “is connected to” is reflective, symmetric, and transitive. Moreover, we define the connected components as a maximal set of objects that are mutually connected. We now implement the following operations.
- Find query, Check if two objects are in the same components.
- Union command. Replace components containing two objects with their union.
Quick find¶
Data structure¶
- integer array
id[N] -
interpretation:
pandqare connected iff they have the same id.i = 0 1 2 3 4 5 6 7 8 9 id=[0, 1, 1, 8, 8, 0, 0, 1, 8, 8] -
Find. Check if
pandqhave the same id. - Union. Change the id of nodes have same id as
pto the id ofq.
Implementation¶
public class QuickFindUF
{
private int[] id;
public QuickFindUF(int N)
{
id = new int[N];
for (int i = 0; i < N; i++)
id[i] = i;
}
public boolean connected(int p, int q)
{ return id[p] == id[q]; }
public void union(int p, int q)
{
int pid = id[p];
int qid = id[q];
for (int i = 0; i < id.length; i++)
if (id[i] == pid) id[i] = qid;
}
}
Complexity¶
| Algorithm | Initialization | Find | Union |
|---|---|---|---|
| Quick Find | N | 1 | N |
Quick find defect¶
- Union is too expensive ( O(N))
- Trees are flat, but too expensive to keep them flat.
Quick union¶
Data structure¶
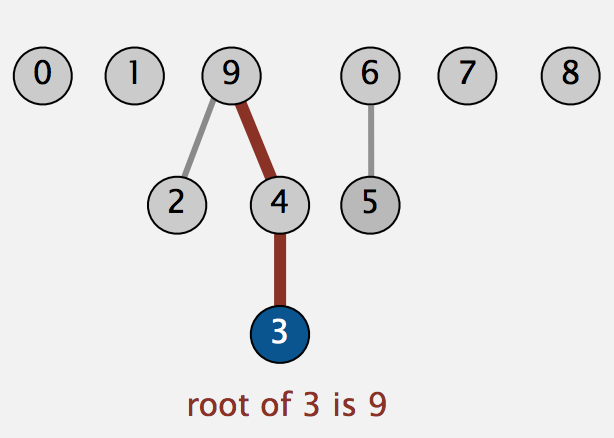
- Integer array
id[N] - Interpretation:
id[i]is parent ofi. -
Root of i is
id[id[id[...id[i]...]]]. (the root’s parent is itself).i = 0 1 2 3 4 5 6 7 8 9 id=[0, 1, 9, 4, 9, 6, 6, 7, 8, 9] -
Find. Check if
pandqhave the same root. - Union. set the id of
p’s root to the id ofq’s root.
Implementation¶
public class QucikUnionUF
{
private int[] id;
public QuickUnionUF(int N)
{
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
}
private int root(int i)
{
while (i != id[i]) i = id[i];
return i;
}
public boolean connected(int p, int q)
{
return root(p) == root(q);
}
public void union(int p, int q)
{
int i = root(p);
int j = root(q);
id[i] = j;
}
}
Complexity¶
| Algorithm | Initialization | Find | Union |
|---|---|---|---|
| Quick Union | N | N | N |
Quick union defect¶
- Trees can get tall
- Find is too expensive O(N)
Improvement by weighting¶
Principles¶
- Modify quick-union to avoid tall trees.
- Keep track of the size of each tree.
- Balance by linking root of the smaller tree to root of the large tree.
Data structure¶
Same as the quick union, but maintain extra array sz[i] to count the number of objects in the tree rooted at i.
- Find. Identical to the Quick Union
- Union. Link root of the smaller tree to root of the larger tree.
Implementation¶
/* weighted quick union */
public void union(int p, int q)
{
int i = root(p);
int j = root(q);
if (i == j) return;
if (sz[i] < sz[j])
{
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
}
Weighted quick-union complexity¶
- Find. takes time proportional to the depth of
pandq. - Union. Take constant time, given root.
| Algorithm | Initialization | Find | Union |
|---|---|---|---|
| Quick Find | N | 1 | N |
| Quick Union | N | N | N |
| Weighted Quick Union | N | lg(N) | lg(N) |
Analysis¶
Proposition. Depth of any node x is at most lg(N)
Proof. When does depth of x increse?
- The depth of x in tree T_1 will increase 1 when it merged with a larger tree.
- How many merges it could possibly happen? Because each merge will double the size of the tree containing x , it can double the tree at most lg(N) times. We can prove that it can merge at most lg(N) times.
Quick union with path compression¶
Principles¶
After computing the root of the p, set the id of each examined node to point to that root.
Implementation¶
/* one-pass solution */
private int root(in i)
{
while (i != id[i])
{
id[i] = id[id[i]]; /* object i's grad parent becomes its parent. */
i = id[i];
}
}
Weighted quick-union with path compression¶
Amortized analysis¶
Proposition. Starting from an empty data structure, any sequence of M union-find ops on N objects makes \leq c(N + Mlg^*N) array access.
- Analysis can be implemented to N + M \alpha(M, N).
- The proof is too complex to be discussed here.
Here is a notation of lg^*, which is the iterate log function. it growing very slow.
In theory, the Weighted Quick Union Path Compression algorithm cost within a constant factor of reading in the data. But not truly linear. In practice, WQUPC is linear.
Summary¶
M union-find operations on a set of N objects
| Algorithm | worst-case time |
|---|---|
| quick find | MN |
| quick union | MN |
| weighted quick union | N+MlgN |
| quick union with path compression | N+MlgN |
| weighted quick union with path compression | N+Mlg^*N |
Problems¶
Number of Islands¶
Longest Consecutive Sequence¶
Surrounded Regions¶
Number of Islands II¶
Graph Valid Tree¶
Number of Connected Components in an Undirected Graph¶
Friend Circles¶
765. Couples Holding Hands¶
Solution 1 Union Find
Briefly, We can view each double seat couch as a node. Each couple in the same couch is a graph node. For those couple not seat in the same couch, we connect the two different couch together. We are looking for valid swaps that remove the inter-counch edge and create a new component in the graph. the conclusion is that we cannot remove two edges by a single swap. This should proof the greedy will work.
Solution 2 Greedy
Notice there is a tick to use here which is XOR a number x with 1 will get you to either x + 1 or x - 1.
x^1 = x + 1, if x is even
x^1 = x - 1, if x is odd
class Solution {
public:
int minSwapsCouples(vector<int>& row) {
int res = 0;
for (int i = 0; i < row.size(); i += 2) {
int x = row[i];
if ((x ^ 1) == row[i + 1]) continue;
res++;
for (int j = i + 1; j < row.size(); ++j) {
if (row[j] == (x ^ 1)) {
row[j] = row[i + 1];
row[i + 1] = (x ^ 1);
break;
}
}
}
return res;
}
};